Встановлення закону вимірювання випадкових величин за результатами дослідження

Національний Технічний Університет України

«Київський політехнічний інститут»

ПРАКТИЧНА РОБОТА

З КУРСУ

«ОСНОВИ НАУКОВИХ ДОСЛІДЖЕНЬ»

ВСТАНОВЛЕННЯ ЗАКОНУ ВИМІРЮВАННЯ ВИПАДКОВИХ ВЕЛИЧИН ЗА РЕЗУЛЬТАТАМИ ДОСЛІДЖЕННЯ

Виконала:

Студентка V курсу ММІ

групи МЛм-61

Першак Н.С.

Залікова книга

№ МЛ-6115

Київ 2010

1.  ПОБУДОВА ЕМПІРИЧНОЇ КРИВОЇ

Таблиця відхилень результатів.D =18мм

Таблиця 1

№	х	№	х	№	х	№	х	№	Х
101	0,034	111	-0,059	121	-0,055	131	-0,055	141	-0,046
102	0,055	112	-0,022	122	-0,041	132	-0,095	142	0,027
103	0,062	113	-0,052	123	-0,03	133	-0,038	143	0,031
104	0,043	114	-0,076	124	-0,056	134	-0,062	144	0,062
105	-0,035	115	-0,048	125	-0,065	135	-0,029	145	-0,046
106	-0,066	116	-0,026	126	0,076	136	-0,035	146	0,032
107	0,034	117	-0,002	127	0,046	137	-0,012	147	0,053
108	-0,046	118	-0,071	128	0,026	138	-0,021	148	-0,049
109	-0,072	119	-0,042	129	0,025	139	-0,055	149	0,035
110	-0,031	120	-0,022	130	0,063	140	0,061	150	0,045

Максимальне відхилення x_imax = +0,076;

Мінімальне відхилення  x_imin = -0,095;

Зона розсіювання  R = |Max| + |Min| = 0,076+0,095 = 0,171 мм.

Розділимо зону розсіювання на 5 груп, з інтервалом h = R/5 = 0,0342 мм.

Таблиця 2

Для графічного зображення емпіричного розподілу будуємо гістограму розподілення. Гістограма зображає диференційний закон розподілення випадкової величини.

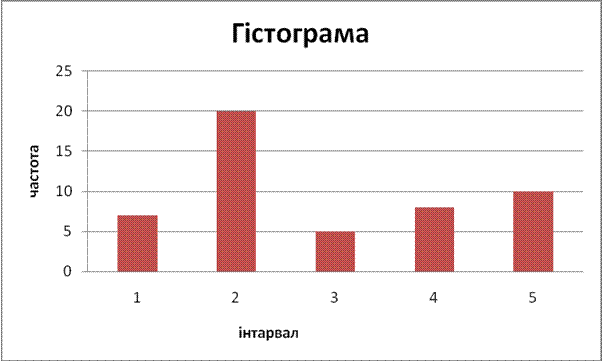
2. ОБЧИСЛЕННЯ ПАРАМЕТРІВ ЕМПІРИЧНОГО РОЗПОДІЛУ

У випадку, коли значення випадкової величини  задані більш ніж двозначними числами і об’єм вибірки , то розрахунок параметрів доцільно вести шляхом введення нової випадкової величини:

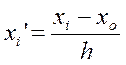
де х’_і – нова випадкова величина;

h – величина інтервалу;

х_о – деяке початкове значення (зазвичай приймають середину середніх значень х_i).

Приймаємо   

Тоді oбчислимо середнє значення, середньо квадратичне відхилення, асиметрію та ексцес.

Розрахунок проведемо на основі даних табл.2. Для цього заповнимо табл.3.

Таблиця 3

№	Інтервали			Середина інтервалу	Нова. випадк. велич
	Від	До
1	-0,095	-0,0608	7	-0,0779	-2	-14	28	-56	112
2	-0,0608	-0,0266	20	-0,0437	-1	-20	20	-20	20
3	-0,0266	0,0076	5	-0,0095	0	0	0	0	0
4	0,0076	0,0418	8	0,0247	1	8	8	8	8
5	0,0418	0,076	10	0,0589	2	20	40	80	160
	Сума		50			-6	96	12	300

Визначаємо початкові моменти  (а₁, а₂, а₃, а₄ ):

а₁ = Σm_ix^'_i / Σm_i = -6/50 = -0,12;