Встановлення закону вимірювання випадкових величин за результатами дослідження, страница 3

В кожне теоретичне розподілення (в його диференціальну чи інтегральну функцію) входить кілька величин, що називаються параметрами (математичне очікування, дисперсія та інші). Так як ці величини невідомі, то їх необхідно визначити по емпіричному розподіленню, підставити в функцію щільності замість теоретичних значень цих величин, а потім розраховувати ймовірності серед усіх інтервалів. Домноживши ці ймовірності на кількість випробувань , отримаємо теоретичне значення частот випадкової величини, які дають вирівняну криву. Для прикладу розглянемо вирівнювання емпіричного розподілу за нормальним законом (Гауса).

Даний закон двухпараметричний. Тому попередньо знаходимо середнє значенняі середнє квадратичне відхилення .

Для обчислення скористаємося даними, що приведенні в табл.3.

Знаходимо

Підставляємо ці значення в функцію щільності, заміняючи на  і на .

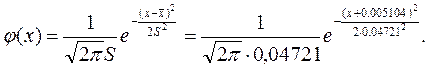
Результати вирівнювання приведенні в табл. 4.

В стовбці 5 знаходиться 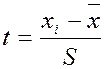, де   - середина i-го інтервалу;

- середнє значення;

- середнє квадратичне відхилення.

По знайденим значенням  в додатку 1 знаходимо значення 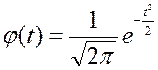, які представленні в стовбці 6.

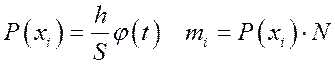
Таблиця 4

Номер інтервалу (№)	Середина інтервалу xi	Емпіричні частоти mi				Ймовірність інтервалів	Теоретичні частоти mi
1	2	3	4	5	6	7	8
1	-0,0779	7	-0,0728	-1,5420	0,1215	0,0880	4,4023
2	-0,0437	20	-0,0386	-0,8175	0,2857	0,2070	10,3478
3	-0,0095	5	-0,0044	-0,0931	0,3973	0,2878	14,3913
4	0,0247	8	0,0298	0,6313	0,3269	0,2368	11,8424
5	0,0589	10	0,0640	1,3557	0,1592	0,1153	5,7659
Сума		50

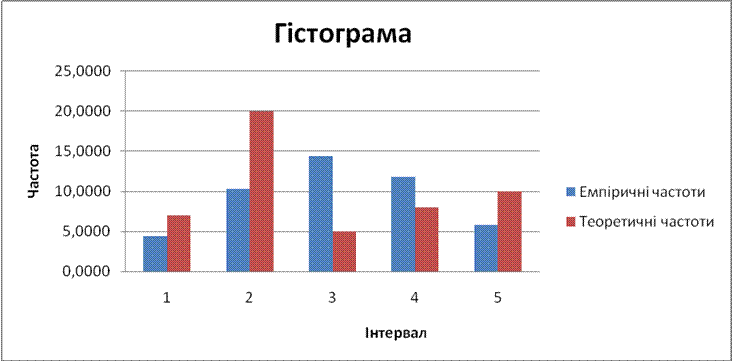
Графіки емпіричної (ряд 1) та вирівняної (ряд 2) кривої:

7.  ПОРІВНЯННЯ ЕМПІРИЧНИХ І ТЕОРЕТИЧНИХ ФУНКЦІЙ РОЗПОДІЛЕННЯ ЧАСТОТ ПО КРИТЕРІЯМ ПОГОДЖЕННЯ

а) Критерій погодженняПірсона

Критерій є найбільш точнішим при більшій кількості спостережень. Його повнота полягає в тому, що він майже завжди відкидає невірну гіпотезу. Він забезпечує мінімальну помилку в прийнятті невірної гіпотези в порівнянні з іншими критеріями. Цей критерій слід застосовувати в ти випадках, коли теоретичні значення параметрів функції розподілення невідомі.

Послідовність обчислень приведена в табл.5

В стовбцях 2 і 3 дані відповідають емпіричні і теоретичні частоти.

Перед тим як робити наступні обчислення, необхідно об’єднати частоти, які зустрічаються менше 5.

Значення

.

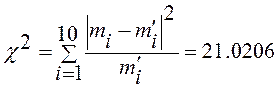Після знаходження величини потрібно знайти число вільності , де к - число степеней вільності;

n - число порівняльних частот (об’єднанні частоти на кінцях приймають за одну частоту);

r - число параметрів теоретичної функції розподілення.

У випадку, який розглядається n= 4, r= 2, так як нормальний заком двухпараметричний. Тому . Далі, використовуючи додаток 2, знаходимо, що для  і , тобто криві узгоджуються погано.