Встановлення закону вимірювання випадкових величин за результатами дослідження, страница 2

а₂ = Σm_i (x^'_i )² / Σm_i = 96/50 = 1.92;

а₃ = Σm_i (x^'_i )³ / Σm_i = 12/50 = 0,24;

а₄ = Σm_i (x^'_i )⁴ / Σm_i = 300/50 = 6;

Обчислюємо центральні моменти :

m₂ = a₂ – a₁ = 1.92– (-0,12) = 2,04;

m₃ = a₃ – 3a₁a₂ + 2a₁³ = 0,24- 3·(-0,12)· 1.92+ 2·(-0,12)³ = 0,9277;

m₄ = a₄ – 4a₁a₃ + 6a₁²a₂ - 3 a₁⁴ = 6,28;

Визначаємо середнє значення та середнє квадратичне відхилення величини   

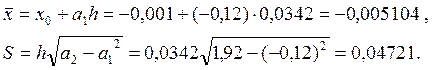
Показник асиметрії: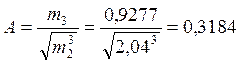             

Показник ексцесу: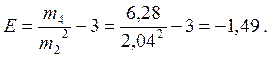             

3. ВИЗНАЧЕННЯ ПОЛЯ ДОПУСКУ ЗА ЕМПІРИЧНИМ РОЗПОДІЛОМ

Багато експериментів проводяться з цілю знаходження поля допуску, яке характерне для даного технологічного процесу і дає ймовірність ризику (браку) не більше деякого наперед заданого числа. Позначимо ймовірність ризику через . Зазвичай приймають  

Задача полягає в тому, щоб вибране поле допуску охопило не менше  99,73% всієї площі, обмеженою генеральною кривою (або деякого іншого раніше заданого числа). Для цього потрібно знайти таке , щоб з заданою ймовірністю, близькою до одиниці (надійність  Р),  містило не менше (1 - 2b) 100% всієї нормальної генеральної сукупності.

 - емпіричне середнє і середнє квадратичне відхилення.

Значення коефіцієнта l розраховані для вибірки з нормальної сукупності.

;

де k – число степенем вільності

Задаємо надійність визначення допуску.  Покладемо, що .  Задаємо ймовірність 1 - 2b, тобто задаємо площу генеральної кривої, яка входить у визначений нами допуск.

Положим 1 - 2b = 1 - 2 . 0,05 = 0,9.

По табл. 7 знаходимо, що для , 1 - 2b = 0,9 і  (приймаємо k  =50). Звідси l = 1,99.

Знаходимо границі поля допуску

;

Находим координату середины поля допуска и половину поля допуска:

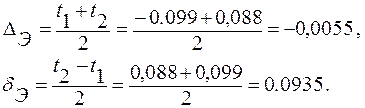
Таким чином, якщо за поле допуску брати величину t₂ - t₁ = 0,187, то з ймовірністю 0,95 з усіх спостережень 90% будуть лежати в цьому в цьому інтервалі.

4. ВИЗНАЧЕННЯ КОЕФІЦІЄНТІВ ВІДНОСНОЇ АСИМЕТРІЇ І ВІДНОСНОГО РОЗСІЮВАННЯ

Для визначення коефіцієнтів a_э, К_э спочатку по виборці знаходять і S, а потім по формулам 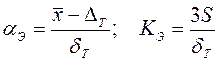 знаходимо значення коефіцієнтів a_э, К_э.

Як було знайдено вище

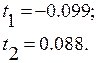
За значеннями  і  знаходимо координату середини поля допуску і половину поля допуску

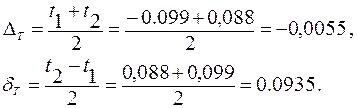
Для даної вибірки обчисленні .

Тоді

;

.

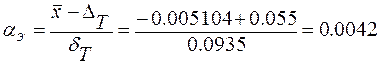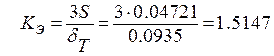
5.  КРИТЕРІЙ ДЛЯ НЕСПРИЙНЯТТЯ РІЗКО ВИДІЛЯЮЧИХСЯ СПОСТЕРЕЖЕНЬ (ПОМИЛКИ ВИМІРЮВАННЯ)

Розглянемо всі отриманні значення відхилень розміру, виміру 132, яке дало значення -0,095. Необхідно перевірити чи є це вимірювання результатом помилки.

Обчислюємо середнє значення з 49 інших результатів (-0,095 відкидаємо)

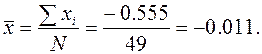
Знаходимо середнє квадратичне відхилення

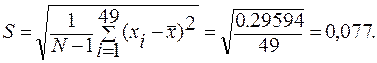
По табл. 8 знаходимо, що для N = 49 і, наприклад,  для b = 0,02 значення    t_b' = 2,456.

Обчислюємо 

Обчислюємо.

Так як 0,084<0,189, то з ймовірністю 1-b =1- 0,02  отримане значення -0,095 можна рахувати випадковим.

Перевіримо, чи є результатом помилки значення 0,076 використовуючи критерій Ірвіна.

Цей критерій заснований на різниці між х_N і x_N+1 результатів  вимірювання, де х_N і x_N+1 два найбільших значення випадкової величини. Функція:

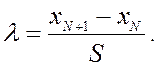
В даному випадку.

Знаходимо і S:

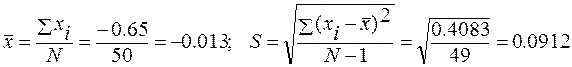
Обчислюємо: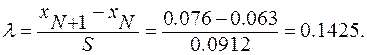 

За табл. 9 знаходимо, що для найближчого N = 50,  . Тому значення x_N+1=0,076 можна рахувати випадковою величиною.

6.  ФУНКЦІЇ ЩІЛЬНОСТІ ТЕОРЕТИЧНИХ І ЕПІРИЧНИХ РОЗПОДІЛЕНЬ

Вирівнювання емпіричного розподілення за гіпотетичним теоретичним

Загальне правило полягає в наступному.