Передаточная функция замкнутой системы для данного примера имеет вид
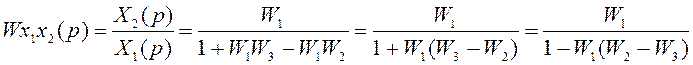
Преобразование структурных схем можно выполнить также с помощью графов, если воспользоваться Таблицей А6. Более полная информация содержится в /14,С. 69-83/.
Методы исследования устойчивости изложены в /4,С. 142-169; 5,С. 89-107; 15,С. 159-178/.
Для установления факта устойчивости системы в домашнем задании используются косвенные методы- критерии устойчивости: Раусса, Гурвица, Михайлова и Найквиста.
В линейных системах устойчивость систем автоматического регулирования определяется только параметрами звеньев и не зависит от возмущения, действующего в системе. А это означает, что для исследования устойчивости по критериям Раусса, Гурвица и Михайлова достаточно взять характеристическое уравнение (знаменатель передаточной функции) замкнутой системы.
При использовании критерия Найквиста об устойчивости замкнутой системы судят по виду амплитудно-фазовой характеристики разомкнутой системы.
Строится амплитудно-фазовая характеристика разомкнутой системы следующим образом.
В выражение передаточной
функции 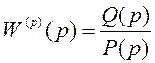 подставляется
подставляется ![]() . Тогда
. Тогда 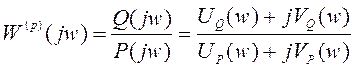 , где
, где
![]() ,
, ![]() - действительная и мнимая части
комплексного выражения
- действительная и мнимая части
комплексного выражения ![]() ;
;
![]() ,
, ![]() - действительная и мнимая части
комплексного выражения
- действительная и мнимая части
комплексного выражения ![]() .
.
Избавляются от
иррациональности в знаменателе путем умножения числителя и знаменателя
комплексной передаточной функции ![]() на
комплексно-сопряженное знаменателю число
на
комплексно-сопряженное знаменателю число ![]() .
.
После несложных
преобразований выделяют действительную и мнимую части комплексной функции ![]() :
:
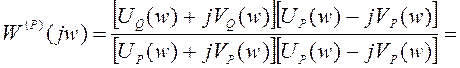
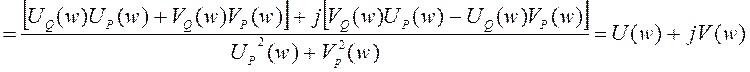
где 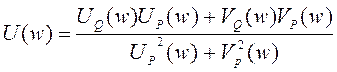 ,
(2.34)
,
(2.34)
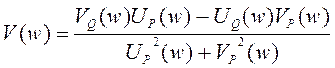 . (2.35)
. (2.35)
Амплитудно-фазовую
характеристику разомкнутой системы строят по точкам, изменяя частоту от ![]() до
до ![]() .
Количество точек должно быть достаточным для определения вида
амплитудно-фазовой характеристики.
.
Количество точек должно быть достаточным для определения вида
амплитудно-фазовой характеристики.
Заключению об устойчивости исследуемой системы должна предшествовать формулировка критерия устойчивости.
2.3 Методические указания к выполнению домашнего задания 3
Целью третьего домашнего задания является закрепление знаний по оценке качества управления в установившихся и переходных режимах работы автоматической системы при типовых внешних воздействиях, а также приобретении практических навыков по расчету основных показателей качества процесса управления различными методами.
Различают два режима работы системы автоматического управления: установившейся и переходный.
Установившейся режим – это такой режим, при котором ошибка системы постоянна во времени.
Переходной режим – это переход системы из одного установившегося состояния в другое под действием приложенного возмущения, либо вследствие ненулевых начальных условий.
Точность системы автоматического управления в установившемся режиме определяется величиной установившейся ошибки.
Точность системы
в переходном режиме определяется величиной переходной ошибки, т.е. величиной
отклонения управляемой переменной X(t) от заданного
значения ![]() и длительностью существования этих отклонений.
и длительностью существования этих отклонений.
Следует различать статический установившейся режим, при котором задающее воздействие не изменяется во времени, и динамические установившиеся режимы, при которых i-я производная от задающего воздействия есть величина постоянная. Соответственно различают статическую и динамическую точность.
Статическую точность оценивают только при анализе статических систем, в основном, систем стабилизации, для которых
![]() и
и ![]() ,
(2.36)
,
(2.36)
где
![]() и
и ![]() -
соответственно задающее и возмущающее воздействия.
-
соответственно задающее и возмущающее воздействия.
Точность статической системы принято оценивать коэффициентом статизма /15.С.147-148 /.
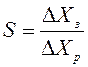 ,
(2.37)
,
(2.37)
где
![]() -
отклонение управляемой величины Х от заданного значения
-
отклонение управляемой величины Х от заданного значения ![]() ,
создаваемое возмущением
,
создаваемое возмущением ![]() при разомкнутом
контуре регулирования;
при разомкнутом
контуре регулирования;
![]() -
отклонение управляемой величины, создаваемое тем же возмущением
-
отклонение управляемой величины, создаваемое тем же возмущением ![]() в замкнутой системе.
в замкнутой системе.
Очевидно, что
![]() ,
(2.38)
,
(2.38)
а
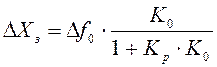 ,
(2.39)
,
(2.39)
где
![]() - коэффициент передачи объекта,
- коэффициент передачи объекта,
![]() - коэффициент усиления регулятора.
- коэффициент усиления регулятора.
Из (2.38) и (2.39) следует, что коэффициент статизма
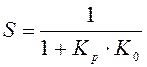 .
(2.40)
.
(2.40)
Коэффициент статизма S иначе еще называется коэффициентом ошибки по положению.
Точность
статической системы считается удовлетворительной, если ![]() ,
что соответствует коэффициенту передачи разомкнутого контура статической
системы
,
что соответствует коэффициенту передачи разомкнутого контура статической
системы ![]() .
.
В астатической системе в статическом режиме ошибки равны нулю.
Динамическая точность систем автоматического управления оценивается по величине сигнала ошибки в установившемся динамическом режиме, который имеет место в следящих системах с астатизмом 1-ого порядка (кинетическая или динамическая ошибки по скорости) и в следящих системах с астатизмом 2-ого порядка (динамическая ошибка по ускорению).
В зависимости от свойств системы и от точки приложения внешнего воздействия вынужденная составляющая сигнала ошибки либо равна постоянной величине (установившаяся ошибка по скорости или по ускорению), либо неограниченно возрастает.
Для нахождения постоянной вынужденной составляющей сигнала ошибки (по скорости или по ускорению) эффективным методом является использование теоремы операционного исчисления о конечном значении оригинала /15.С.150 /. Возрастающую вынужденную составляющую находят при помощи метода коэффициентов ошибок / 5. С. 124-127 /.
Все
установившиеся ошибки (статическая и динамические ошибки по скорости и
ускорению) тем меньше, чем больше коэффициент передачи разомкнутой системы ![]() , так как установившиеся ошибки обратно
пропорциональны К /15. С.151 /.
, так как установившиеся ошибки обратно
пропорциональны К /15. С.151 /.
При анализе точности автоматических систем в установившемся режиме иногда используют такое понятие, как добротность системы D. Добротность D системы в установившемся режиме прямо пропорциональна коэффициенту передачи разомкнутой системы.
Необходимые сведения по изучению статической и динамической точности систем можно найти, например, в /3.С.281-295; 4.С.188-200; 5.С.61-64 /, а также в конспекте лекций.
Точность системы в переходных режимах можно оценить с помощью прямых и косвенных методов.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.