Прямые методы – это методы расчета на современных ЭВМ переходной характеристики h(t) (реакция системы на самое «тяжелое» воздействие – единичное ступенчатое), по которой непосредственно (прямо) оценивается качество управления в переходном режиме.
Прямые (точные) методы условно можно разбить на две группы: методы численного интегрирования и методы структурного моделирования.
При численном интегрировании система управления представляется в виде совокупности дифференциальных уравнений, при структурном моделировании – в виде структурной схемы, состоящей из элементарных динамических звеньев.
Однако чаще всего целесообразнее для предварительной оценки качества переходного процесса воспользоваться либо косвенными методами, либо приближенными методами расчета переходной функции h(t), не прибегая к расчетам на ЭВМ. Одним из таких простых методов является метод трапеций, предложенный В.В. Солодовниковым и А.А. Вороновым.
Приближенные методы для получения h(t) базируются на использовании частотных характеристик и справедливы для минимально-фазовых систем.
При выполнении домашнего задания 3 следует хорошо изучить методику построения логарифмических амплитудно и фазо-частотных характеристик разомкнутых систем по передаточным функциям в /3.С.88-89; 5.С.84-88; 7,4.1.С.269-270; 12.С.196-199 / или в других учебниках и пособиях по теории автоматического управления.
Логарифмическая амплитудно-частотная характеристика (ЛАЧХ) должна быть асимптотической, а фазо-частотная характеристика (ЛФЧХ)- непрерывной.
Если ЛАЧХ и ЛФЧХ
определенны с помощью ЭВМ, то непрерывную ЛАЧХ необходимо представить в виде
совокупности асимптот, предварительно нанеся на ось 
частоты
сопряжения асимптот.
Логарифмические амплитудно и фазо-частотные характеристики разомкнутой системы позволяют определить запасы устойчивости в замкнутой системе /5.С.104-106; 12.С.245-248 /, построить вещественную частотную характеристику замкнутой системы по ЛАЧХ и ЛФЧХ разомкнутой системы с помощью номограммы /5.С.119-121; 4.С.206-208; Приложение Б, рис. Б1 /.
Приближенный метод построения переходной функции h(t) с помощью вещественных трапециидальных частотных характеристик (метод трапеций) изложен в /4.С.200-206; 5.С.114-119; 14.С.447-448 /. Таблица h-функций приведена также в приложении А, таблицы А7.
Сведения о показателях качества переходного процесса можно найти в /4.С.181-185; 5.С.107-109; 15.С.195-200 /.
2.4 Методические указания к выполнению домашнего задания 4
Целью четвертого домашнего задания является закрепление знаний по способам коррекции систем автоматического управления для достижения требуемого качества процесса управления в установившемся и переходном режимах, а также приобретение практических навыков по синтезу корректирующих устройств.
В системе автоматического управления может быть явно выделена неизменяемая часть и оставшаяся изменяемая часть системы, в которую можно вносить коррективы и обеспечивать требуемое качество процесса управления. Неизменяемая часть системы, как правило, ограничивает возможность получения требуемого качества и в изменяемую часть системы для достижения нужного качества иногда требуется вносить нереализуемые корректирующие устройства. Задача синтеза существенно сложнее, чем задача анализа (моделирования) системы.
При синтезе корректирующих устройств (регуляторов) в замкнутых системах автоматического управления приходится решать проблему фундаментального противоречия – противоречия между точностью системы в установившемся режиме и запасами устойчивости в переходном режиме.
Качество процесса управления можно существенно повысить, если идти по пути синтеза структуры системы управления, обеспечивающей оптимальные значения показателей качества процесса управления, например, минимума времени переходного процесса, минимума ошибки управления и т.п. В данном случае используются методы теории вариационного исчисления и интегральные оценки качества.
В домашнем задании 4 Вы будете идти по пути коррекции известной структуры с целью получения требуемых (неоптимальных) показателей качества процесса управления.
Теория управления дает набор стандартных методов синтеза систем с заданным качеством. Классическим методом этого ряда является метод диаграмм В.В.Солодовникова. (Приложение Б, рис.Б2).
На рис.Б2, а, б,
и в представлены обобщенные номограммы Солодовникова /14 /, с помощью которых
можно определить частоту среза 
по показателям
максимального перерегулирования 
и времени регулирования
. При использовании номограмм
Солодовникова по характеристике 
(рис.Б2, а)
определяют следующие параметры:
; 
; 
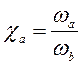и
.
Номограмма на рис.Б2,б построена для следующих параметров:
; 
и 
,
а на рис.Б2,в при
; 
;
и 
.
Для определения частоты среза
используют эмпирическую формулу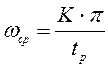 
.
Если 
,
а 
,то пользуясь номограммой (рис.Б2,б),
для системы с астатизиом 1-ого порядка, получим 
,
откуда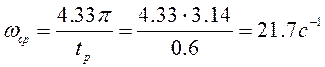 
.
Необходимый для изучения материал изложен в учебниках и учебных пособиях, приведенных в списке рекомендуемой литературы, на которую даны ссылки в методических указаниях.
В частности, при изучении необходимости и способов коррекции систем руководствуйтесь источниками /5.С.130-151; 7.С.237-269; 14.С.609-659; 15.С.234-263 /.
При выполнении
пунктов 
изучите и используйте материал,
представленный в /7.С.268-282; 8.С.249-260; 12.С.366-374; 14.С.622-627;
17.С.185-209 /.
При коррекции решаются следующие частные задачи:
- стабилизация неустойчивых систем;
- повышение запасов устойчивости (демпфирование колебаний);
- повышение статической и динамической точности в установившемся режиме;
-улучшение качества переходного процесса.
В зависимости от требований к системе одни задачи становятся основными, другие - второстепенными.
Перечисленные частные задачи могут быть решены по отдельности или совместно с помощью того или иного способа коррекции путем введения в систему дополнительных устройств, называемых корректирующими.
В последнее время, благодаря целому ряду достоинств, получила широкое распространение последовательная коррекция и ее техническая реализация на базе активных корректирующих устройств.
Если требования к системе не очень жесткие, то можно использовать пассивные корректирующие устройства.
Принципиальные схемы и передаточные функции пассивных и активных корректирующих устройств широко представлены в /17.С.194-196,С.206-209; 14.С.636-658 /.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.