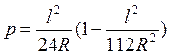Нивелирование трассы: Методические указания к выполнению расчетно-графической работы, страница 7

                                ,                                                 (4.4)

Тp = ptg(a¤2);   Бp = psec(a¤2),                                     (4.5)

Длина сложной кривой будет равна:

 Кc = R (a-2b) + 2l =  Ra - 2Rb + 2l =  K -l + 2l = K + l.              (4.6)

Домер сложной кривой равен:

Д с = 2Тс - Кс = Д + Дp= Д  + 2(m + Tp) - l.                         (4.7)

Элемент Дp вычисляют по формуле

  Дp = 2·Tp- 2(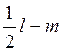)  или    Дp= 2·( m+ Т_p) - l                     (4.8)

Пример.

Дано: угол поворота a = 19°12¢, радиус круговой части кривой R = 800 м и длина переходной кривой l = 80 м. Вершина угла расположена на  ПК 17 + 35,90.

Сначала по формулам (4.1) или по таблицам  [1 или 2] находим элементы  круговой кривой:

Т = 135,31 м; К = 268,08 м; Д = 2,54 м; Б = 11,36 м.

Затем по формулам (4.3 – 4.5) вычисляем или находим по таблицам приращения соответствующих элементов сложной  кривой:

Т_p = 0,06 м;  m = 40,00 м; Б_p = 0,34 м; Д_p = 0,11 м.

Теперь вычисляем суммированные значения:

Tс = T + m + T_p = 135,31 + 40,00 + 0,06 = 175,37 м;

Кc = K + l = 268,08 + 80, 00 = 348,08 м;

Бс = Б + Б_p = 11,36 + 0,34 = 11,70 м;

Дс = Д + Д_p= 2,54 + 0,11 = 2, 65 м.

Контроль вычислений. Д с = 2Тс - К с = 2·175,37 - 348,08 = 2,66 м

Расхождение с вычисленным ранее значением Дс не должно превышать   0,02 м.

При пользовании таблицами [1 или 2] элементы кривой выбирают из таблицы 1 «Элементы круговых и переходных кривых».

Верхняя часть таблицы содержит элементы круговой кривой. Аргументами здесь являются  R – радиус круговой кривой (приведен в правом верхнем углу страницы) и a - угол поворота (крайний левый столбик). Элементы кривой приведены с интервалом 3´. Рядом с каждым элементом кривой (Т, К, Д, Б) даны величины  ΔТ, ΔК, ΔД и ΔБ  - изменения соответствующего элемента на 1´. Для R = 1000 м и R = 100 м эти поправки выражены в миллиметрах, для остальных радиусов – в сантиметрах.

Чтобы получить значения элементов кривой для промежуточных значений, выбирают значение элемента, ближайшее к заданному углу a (оно будет отличаться на 1´), затем из соседнего столбика выбирают поправку. Если заданный угол больше табличного, поправку прибавляют, если заданный угол меньше табличного - вычитают.

Далее выбирают  элементы переходной кривой m, и приращения элементов круговой кривой Т_pи Б_p. Они помещены внизу той же страницы. Эти элементы выбирают по величине  l – длине переходной кривой.

Если в таблице указаны два значения элемента Т_pили Б_p, то для заданного угла поворота эти элементы находят интерполяцией в зависимости от местоположения угла поворота a в основной (верхней) таблице.

Для нашего примера. a = 19°12', R = 800 м, l = 80 м.

Таблицы [1], стр.216.

Т = 135,31 м;

К = 268,08 м;

Д =  2,54 м;

Б =  11,36 м.                               

Теперь из нижней части таблицы из  строкиl= 80 выбираем элементы переходной кривой. Для  Tp приведены два значения (0,05 – 0,06). Первое значение дано для угла α = 18°, с которого начинается основная таблица, а второе – для α = 19°30´, которым  оно заканчивается. Поскольку заданный угол поворота расположен в нижней части основной таблицы, то выбираем Tp = 0,06 м; m = 40,00 м; Бp = 0,34 м. Величину Дp вычисляем по формуле (4.8) Дp = 0,12 м.

Далее по формулам (4.2, 4.6 - 4.8) вычисляем элементы сложной кривой.

4.3.  Вычисление пикетажного положения главных точек кривых

Вычислив элементы сложной кривой, приступают к вычислению   пикетажного положения главных точек кривой. Его находят из выражений:

ПК НК = ПК ВУ - Tс;

                                             ПК КК = ПК НК + Кс;                                    (4.9)                                                

ПК СК = ПК НК + Кс /2.                              

Правильность вычислений контролируют по формулам:

ПК КК = ПК ВУ + Tс - Дс;

ПК СК = ПК ВУ + Дс /2.                                (4.10)