Определение показателей качества процесса управления, страница 5

                                                                                   (9.8)

где

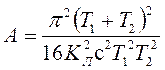                                                                                         (9.9)

Дискриминант уравнения (9.8)

                                                    .                                         (9.10)

Согласно [1,с.319] если система уравнений (9.5) не имеет положительных действительных корней  и , то автоколебания невозможны.

В соответствии с выражением (9.6)  - положительный действительный корень системы (9.5). С другой стороны, уравнение (9.8) будет иметь действительные корни  только в том случае, если дискриминант , т.е. если

                                                             (9.11)

или

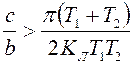                                                   .                                        (9.12)

Если выполняется условие (9.11), то уравнение (9.8) имеет два действительных решения. Для того, чтобы установить, которое из двух решений соответствует устойчивым колебаниям, необходимо воспользоваться общим условием устойчивости автоколебаний

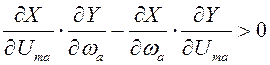                            .                             (9.13)

Для нашего случая имеем следующую систему уравнений:

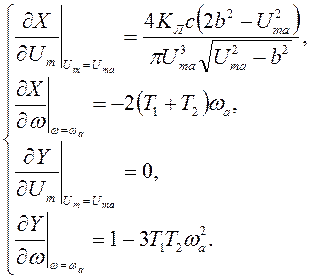                                                   (9.14)

Подставив значения частных производных (9.14) в условие (9.13) и учитывая (9.6), получим

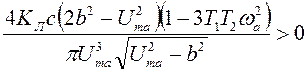                                                   (9.15)

или

                                                                                                 (9.16)

При отсутствии зоны нечувствительности, т.е. при , уравнение (9.8) всегда имеет одно действительное решение

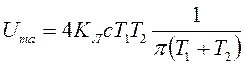                                                                          (9.17)

и в системе всегда будут возникать устойчивые автоколебания.

9.2 Исходные данные

Исходные данные для выполнения исследований приведены в табл. 9.1.

Таблица 9.1 – Параметры исследуемой системы

Параметр	Вариант
	1	2	3	4	5	6	7	8	9	10
T1, c	0,1	0,2	0,3	0,4	0,5	0,6	0,7	0,8	0,9	1,0
T2, c	0,2	0,2	0,2	0,2	0,2	0,2	0,2	0,2	0,2	0,2
K1	3,3	3,3	3,3	3,3	3,3	3,3	3,3	3,3	3,3	3,3
K2, c-1	1	1	1	1	1	1	1	1	1	1
K3	1	1	1	1	1	1	1	1	1	1
U0, В	30	30	30	30	30	30	30	30	30	30

9.3 Программа работы

9.3.1 В соответствии с заданным вариантом (см. табл. 9.1) по формуле (9.6) определите частоту автоколебаний.

9.3.2 Рассчитайте, используя неравенство (9.12), ширину зоны нечувствительности нелинейного элемента. Возьмите значение параметра В.

9.3.3 Определите из выражения (9.8) амплитуды возможных автоколебаний и по неравенству (9.16) проверьте при какой амплитуде возникнут устойчивые автоколебания.

9.3.4 Проведите эксперимент при подаче на вход системы В.

9.3.5 По экспериментальной кривой переходного процесса определите амплитуду и частоту автоколебаний и сопоставьте их с расчетными значениями.

9.3.6 Определите экспериментально значение коэффициента передачи линейной части K_Л, при котором не выполняется условие возникновения автоколебаний.

9.3.7 Установите b=0. Снимите кривую переходного процесса и определите частоту и амплитуду автоколебаний. Экспериментальное значение амплитуды автоколебаний сравните с расчетным значением, найденным по выражению (9.17).

Пункты 9.3.1 – 9.3.3 следует выполнить в процессе самостоятельной подготовки к лабораторной работе во внеаудиторное время.

9.4 Содержание отчета

Отчет о лабораторной работе должен содержать:

1) тему и цель работы;

2) структурную схему системы управления и ее параметры, передаточные функции и схемы моделей;

3) расчеты;

4) графики переходных процессов;

5) результаты эксперимента;

6) выводы по работе.

9.5 Контрольные вопросы

9.5.1 Какая автоматическая система называется нелинейной?

9.5.2 Назовите основные виды нелинейных элементов.

9.5.3 Какими параметрами характеризуется выходной сигнал нелинейной системы в режиме автоколебаний?

9.5.4 Покажите как с помощью критерия Михайлова определяется амплитуда и частота автоколебаний.

9.5.5 В каких случаях автоколебания можно отыскать при помощи критерия Найквиста?

9.5.6 Назовите условия существования автоколебаний по критерию Михайлова, по критерию Найквиста?

9.5.7 Как с помощью критерия Найквиста определяется амплитуда и частота автоколебаний?

9.5.8 Зависит ли устойчивость нелинейной системы от величины внешнего воздействия?

9.5.9 Какие задачи решаются при анализе нелинейных систем?

9.5.10 Как определить по графику фазовой траектории амплитуду и частоту автоколебаний?

Список литературы

1. Лукас В.А. Теория автоматического управления: Учеб. для вузов. – 2-е изд., перераб. и доп. – М.: Недра, 1990. – 416 с.

2. Зайцев Г.Ф. Теория автоматического управления и регулирования. - 2-е изд., перераб. и доп. - Киев: Вища шк., 1989.- 431 с.

3. Топчеев Ю.Н. Атлас для проектирования систем автоматического регулирования: Учеб. пособие для втузов. – М.: Машиностроение, 1989. – 752 с.