Определение показателей качества процесса управления, страница 3

7.3 Содержание отчета

Отчет о лабораторной работе должен содержать:

1) тему и цель работы;

2) структурную схему, передаточные функции и схему моделирования скорректированной системы;

3) расчеты по синтезу последовательного КУ;

4) электрическую схему КУ и расчет его параметров;

5) графики переходных процессов в исходной, скорректированной и скорректированной оптимизированной системах и оценки их работы (значения показателей качества);

6) ЛАЧХ разомкнутой оптимальной системы и ЛАЧХ КУ при  и , соответствующих оптимизированной настройке.

7) выводы по работе.

7.4 Контрольные вопросы

1. Для чего необходима коррекция автоматических систем?

2. Назовите способы коррекции и дайте им сравнительную оценку.

3. Какие необходимы исходные данные для синтеза корректирующих устройств и как они используются?

4. Желаемая ЛАЧХ и методика ее построения.

5. Изложите методику синтеза последовательного корректирующего устройства.

6. Как по ЛАЧХ определяется передаточная функция?

7. Как находится передаточная функция и рассчитываются параметры корректирующего устройства типа R-С?

8. Назовите основные показатели качества переходных процессов.

9. Нарисуйте типовые ЛАЧХ разомкнутых систем.

10. Как пользоваться номограммами для определения показателей качества замкнутых систем по ЛАЧХ разомкнутых систем.

Список литературы

1. Иващенко Н.Н. Автоматическое регулирование. - М.: Машиностроение, 1978. - 736 с.

2. Теория автоматического управления /Под ред. А.В.Нетушила. - М.: Высш. шк., 1976. - 400 с.

3. Попов Е.П. Теория линейных систем автоматического регулирования и управления. - М.: Наука, 1978. - 255 с.

4. Зайцев Г.Ф. Теория автоматического управления. – К.: Вища шк., 1988. - 430 с.

8 ЛАБОРАТОРНАЯ РАБОТА №7

ИССЛЕДОВАНИЕ ДИСКРЕТНОЙ СИСТЕМЫ УПРАВЛЕНИЯ

Цель - знакомство с работой дискретных систем, определение показателей качества.

8.1 Методические указания

8.1.1 Методические указания по теоретической подготовке к лабораторной работе.

Изучите принцип работы дискретных систем и назначение их основных элементов [1, с.283-293].

8.1.2. Методика проведения эксперимента

Декретная система отличается от непрерывной тем, что часть сигналов в этих системах представляет собой последовательность импульсов или цифровых кодов. Процесс преобразования непрерывного сигнала в дискретный называется квантованием, а время между последовательными импульсами  - интервалом или периодом квантования ( - называется частотой квантования или дискретизации).

Система, для которой дискретный сигнал принимает мгновенные значения непрерывного сигнала  называется импульсной.

Импульсный элемент представляется состоящим из двух частей: идеального ключа и формирователя (рис. 8.1).

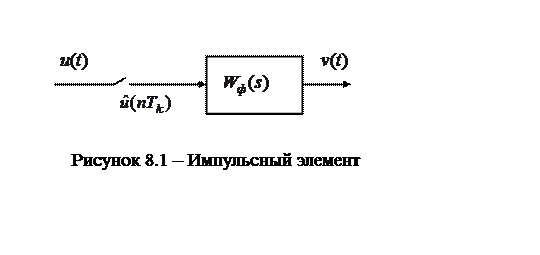Графики сигналов в различных точках схемы (рис. 8.1) представлены на рисунке 8.2 и могут быть описаны следующими выражениями.

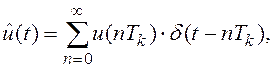                                                                        (8.1)

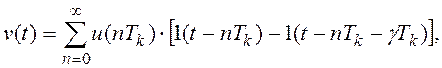                                            (8.2)

где          - дельта-функция;

                 - единичная ступенчатая функция;

                 - относительная длительность импульса;

                             - абсолютная длительность импульса.

В изображениях по Лапласу выражения (8.1) и (8.2) примут вид:

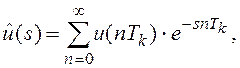                                                                             (8.3)

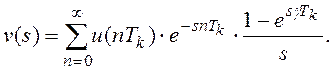                                                              (8.4)

Поделив изображение выходного сигнала  на изображение входного сигнала формирователя , получим передаточную функцию формирователя .

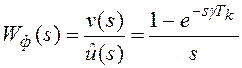                                          .                                  (8.5)

При относительной продолжительности импульса равной единице () получим передаточную функцию формирователя, который известен как экстраполятор нулевого порядка:

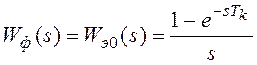                                         .                                (8.6)

Как видно из предыдущего, функция импульсного элемента, состоящего из идеального ключа и экстраполятора нулевого порядка (8.6), заключается в передаче на свой выход в течении всего периода квантования сигнала, величина которого соответствует мгновенному значению входного сигнала в начальный момент периода квантования.

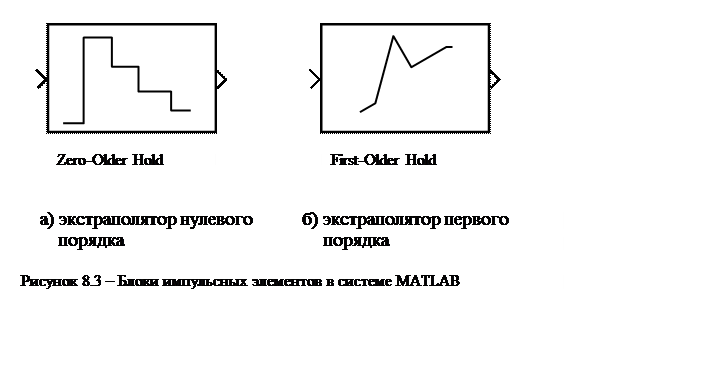
В практике импульсных систем получили распространение импульсные элементы с экстраполяторами не только нулевого, но и более высоких порядков. Выходной сигнал таких элементов зависит не только от мгновенных значений входного сигнала, но и от мгновенных значений первой, второй и т.д. производных этого сигнала. Например, экстраполятор первого порядка задает линейное изменение выходного сигнала на каждом такте дискретизации, в соответствии со скоростью изменения входного воздействия в момент замыкания идеального ключа (рис. 8.3)

Моделирование работы импульсных элементов с экстраполяторами нулевого и первого порядков в системе MATLAB может быть осуществлено с помощью блоков Zero-Older Hold и First-Older Hold, входящих в библиотеку Discrete пакета Simulink (рис. 8.3). Единственным изменяемым параметром данных блоков является период квантования.

В данной лабораторной работе следует провести сравнительное исследование непрерывной замкнутой системы (рис. 8.4) и аналогичных импульсных систем содержащих экстраполяторы нулевого и первого порядков. Система на рисунке 8.4 состоит из объекта второго порядка с передаточной функцией

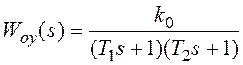                                                                            (8.7)

и пропорционально-интегрального регулятора с передаточной функцией

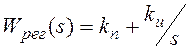                                                                                      (8.9)