Информатика и выч. техника \ Теория автоматического управления

Определение показателей качества процесса управления, страница 4


Согласно предписанию модульного оптимума оптимизации передаточная функция регулятора  при условии, что  - большая постоянная времени, а  - некомпенсируемая малая постоянная времени (), будет равна

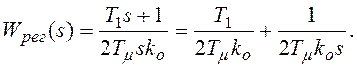                                                        (8.10)

Тогда коэффициенты пропорциональной  и интегральной  частей регулятора можно записать в виде

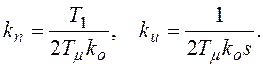                                                                       (8.11)

8.2 Программа работы

8.2.1 Используя пакет программ Simulink системы MATLAB исследуйте работу импульсных элементов, представленных на рисунке 8.3. В качестве тестового входного сигнала примите синусоидальный сигнал единичной амплитуды частотой . Следует получить графики входного, выходного сигналов и сигнала ошибки квантования при различных периодах дискретизации

                              .

Сделайте выводы о влиянии периода квантования на качество работы импульсного элемента.

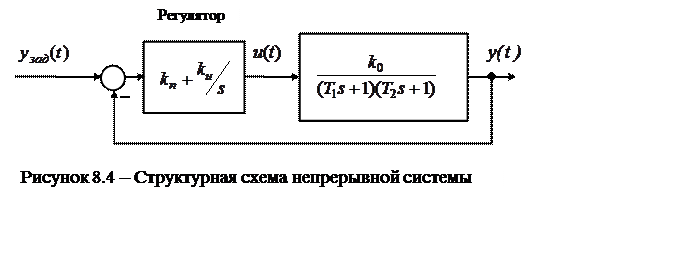
8.2.2 Осуществите моделирование непрерывной системы управления (рис. 8.4) и определите показатели качества перходного процесса при единичном скачкообразном задающем воздействии. Очевидно, что время интегрирования должно быть больше времени достижения первого максимума после начала переходного процесса, т.е. больше  и меньше .

Параметры систем управления для каждой бригады указаны в таблице 8.1.

Таблица 8.1 – Параметры модели согласно вариантов

Номер варианта

1

5

0,5

0,05

2

10

0,4

0,04

3

15

0,3

0,03

4

20

0,2

0,02

5

25

0,1

0,01

6

30

0,7

0,07

7

22

0,8

0,08

8

28

0,9

0,09

9

14

1,1

0,11

10

12

1,2

0,12

8.2.3 Осуществите моделирование импульсной системы управления с экстраполятором нулевого порядка, установленным на выходе регулятора, и определите показатели качества переходного процесса при различных периодах квантования

                              .

Здесь  - частота среза замкнутой системы, которая при модульном оптимуме оптимизации определяется в виде

                                                       .

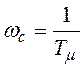8.2.4 Аналогично пункту 8.2.3 исследуйте систему с экстраполятором первого порядка.

Сделайте выводы о влиянии периода квантования на качество работы импульсных систем управления.

8.3 Содержание отчета

Отчет о лабораторной работе должен содержать:

а) тему и цель работы;

б) структурную схему непрерывной системы управления и ее параметры;

в) схемы моделей непрерывной и двух импульсных систем в среде пакета Simulink;

г) кривые переходных процессов и таблицу со значениями показателей качества различных систем при различных периодах квантования;

д) анализ результатов исследования по каждому пункту программы работы и общие выводы о работе.

Список литературы

1. Теория автоматического управления / Под ред. А.В. Нетушила. – М.: Высш. шк., 1979. – 400 с.

2. Дьяконов В.П. Simulink 4. Специальный справочник. – СПб: Питер, 2002. – 528 с.

9 ЛАБОРАТОРНАЯ РАБОТА №8

ОПРЕДЕЛЕНИЕ  АМПЛИТУДЫ  И  ЧАСТОТЫ  АВТОКОЛЕБАНИЙ В  НЕЛИНЕЙНОЙ  СИСТЕМЕ  АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ

Цель работы – теоретическое и экспериментальное определение параметров автоколебаний в нелинейной системе автоматического управления.

9.1 Теоретическая подготовка

Изучите подраздел 9.4 [1, с.313-322]. Можно воспользоваться также [2, с.315-330],  [3, с. 524-529].

Амплитуду и частоту автоколебаний в нелинейной системе, представленной на рис.9.1, можно определить несколькими способами. Ниже рассматривается способ, базирующийся на использовании метода гармонической линеаризации в сочетании с критерием устойчивости Михайлова.

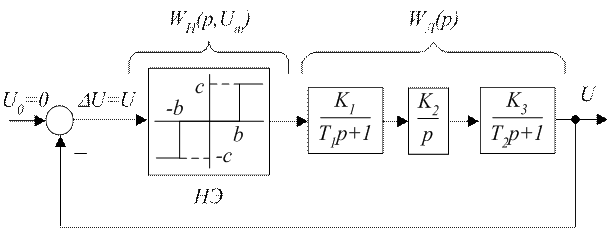
Рисунок 9.1 – Структурная схема нелинейной системы

Передаточная функция линейной части нелинейной системы автоматического управления (см. рис.9.1) имеет следующий вид:

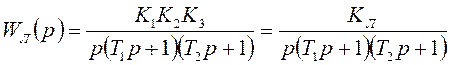                  ,                (9.1)

где KЛ – коэффициент передачи линейной части;

T1 и T2 – постоянные времени инерционных звеньев линейной части системы;

U0 – задающее напряжение;

U – выходное напряжение нелинейной системы.

Эквивалентная передаточная функция нелинейного элемента – трехпозиционного реле равна

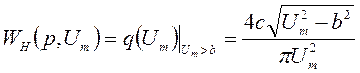                    ,                       (9.2)

где b и c – параметры нелинейности, В;  Um – амплитуда ошибки, В.

Передаточная функция замкнутой гармонически линеаризованной системы

                         ,                            (9.3)

Откуда находим характеристическое уравнение гармонически линеаризованной системы

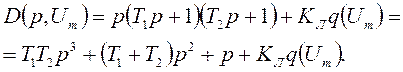                                                  (9.4)

Существование в нелинейной системе автоколебаний соответствует нахождению линеаризованной системы (9.4) на колебательной границе устойчивости.

Колебательную границу устойчивости находим, используя критерий Михайлова. Для этого в уравнение (9.4) подставляем  и приравниваем его действительную и мнимую части к нулю

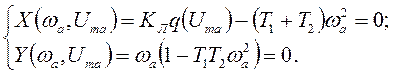                                       (9.5)

Из второго уравнения системы (9.5) можно определить частоту автоколебаний

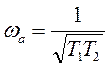                                                      .                                            (9.6)

Из (9.6) видно, что  зависит от постоянных времени.

Подставив значение  в первое уравнение системы (9.5), получим уравнение с одним неизвестным – амплитудой  :

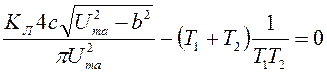                       ,                          (9.7)

Которое приводим к виду

Скачать файл