Определение параметров кодируемого сигнала. Определение параметров кода. Построение кодера в циклический (n, k) код, страница 9

Аналогично строится СФ, согласованный с комбинацией символов ШПС, передающих символ «1» циклического кода (рис. 11, табл. 9):

Рис. 11.

Т а б л.  9.

Заметим, что если импульсную характеристику фильтра, например, взять как у другого фильтра (у СФ с «0» взять ИХ от СФ с «1» или наоборот), то получим, что максимальное значение функции автокорреляции в обоих случаях будет равно 2, и РС, настроенная на значение, равное 3, не пропустит сигнал дальше.

Следовательно, прием будет произведен правильно и сигналы «0» и «1» циклического кода будут различаться друг от друга при приеме.

·  В заключение рассчитаем значения соотношения «сигнал – помеха» при посимвольном приеме и приеме в целом.

Расчет произведем для цифровых СФ. Они являются оптимальными, так как обеспечивают максимальное соотношение «сигнал – помеха» на выходе, равное

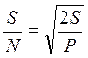                                                                  (21)

Эта формула работает только в случае аддитивной гауссовской помехи (см. п. 5 задания).

Здесь S – мощность (средняя мощность) полезного сигнала; P – мощность помехи (указана в п. 5).

Мощность сигнала можно оценить с помощью функции автокорреляции. Как известно, максимальное значение R (τ) в момент времени, равный Т_с, характеризует энергию сигнала.

Заметим, что в нашем случае не нужно искать отдельно значения соотношения «сигнал – помеха» при посимвольном приеме и приеме в целом, т.к. они будут одинаковы. Это объясняется тем, что максимумы функции автокорреляции одинаковы и при приеме «1», и при приеме «0» циклического кода.

Рассчитаем это в случае посимвольного приема. Умножив условное значение максимума функции автокорреляции на амплитуду импульсов, получим численное значение энергии, переносимой каждым символом циклического кода:

Е_с = 3 ∙ 11,36 мВ = 34,08 мДж.

Зная, что таких символов всего n, т.е. 7, и зная общую длительность передачи сообщения, определим длительность прохождения каждого символа:

Т_с = 23 с / 7 = 3,29 с.

Определим мощность:

S_с = Е_с / Т_с = 34,08 / 3,29 = 10,36 мВт.

Подставляя в формулу (21) это значение, находим:

2,4.

СПИСОК ЛИТЕРАТУРЫ

1. Г о р е л о в  Г. В., Ф о м и н  А. Ф.,  В о л к о в  А. А.,  К о т о в   В. К. Теория передачи сигналов на железнодорожном транспорте. Учеб. для вузов ж.-д. трансп. М., Транспорт, 1999. 415 с.

2. Конспект лекций.