Определение параметров кодируемого сигнала. Определение параметров кода. Построение кодера в циклический (n, k) код, страница 4

Основой для построения схемы деления является производящий полином g(х). Количество элементов памяти равно старшей степени g(х), т.е. 3, а количество сумматоров равно числу знаков сложения в g(х), т.е. 2. Если коэффициент при каком-либо слагаемом g(х) равен 1 (слагаемое присутствует), то там ставится сумматор; в противном случае сумматор не ставится (см. рис. 3).

Работу кодера удобно иллюстрировать с помощью уравнений состояний и таблицы состояний элементов памяти.

Для того, чтобы составить уравнения состояний элементов памяти, введем символ D – «задержка на один такт». Тогда, в соответствии со схемой, можно записать следующие уравнения состояний выходов триггеров:

S1 = D(l + S2 + S3);

S2 = DS1;                                                                                                                                    (10)

S3 = DS2.

Сложение производится по модулю два.

По уравнениям состояний можно составить таблицу состояний (см. табл. 2):

                           Т а б л. 2.

№ такта	К	l	S1	S2	S3	S2+S3	v
1	«1»	1	0	0	0		1
2		0	1	0	0		0
3		0	0	1	0		0
4		1	1	0	1		1
5	«2»	0	0	1	0	1	1
6		0	0	0	1	1	1
7		0	0	0	0	0	0
8		0	0	0	0	0	0

Из таблицы видно, что полученная кодовая комбинация совпадает с теоретической, полученной нами ранее.

4.  ПОСТРОЕНИЕ ГЕНЕРАТОРА СИНДРОМОВ

Перед тем, как построить генератор синдромов (ГС), определим сначала теоретические синдромы ошибок.

Основным принципом при построении синдромов ошибок является следующее. Если сигнал принят без ошибок, то деление кодовой комбинации v(х) на производящий многочлен g(х) должно производиться без остатка. Если же информация принята с ошибками, то в результате ошибок возникает остаток, называемый синдромом ошибки.

В нашем случае в канале действуют ошибки 1-й и 2-й кратности. Определим теоретически синдромы, которые должен вырабатывать ГС при наличии ошибок.

Это производится при помощи деления так называемого вектора ошибки на производящий полином. Длина вектора ошибки равна n, а число в нем единиц определяется кратностью ошибки. Полученный остаток и есть теоретический синдром ошибки.

1) Рассмотрим случай, когда в канале имеется одиночная ошибка. Сформируем вектор ошибки:

Е₁ = 1000000; е₁(х) = х⁶.

Произведем деление на производящий полином:

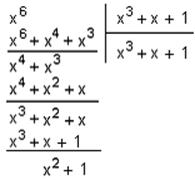
Полученный остаток С_1т(х) = х² + 1 и есть синдром одиночной ошибки.

У этого синдрома есть недостаток, заключающийся в том, что он своим видом не повторяет кратность ошибки (т. к. имеется два слагаемых). Поэтому его нужно модифицировать, т.е. устранить этот недостаток. Для этого перед операцией деления комбинация вектора ошибки сдвигается на (n – k) разрядов влево:

е’(х) = х⁶ ∙ х^7-4 = х⁹.

Снова производим деление:

Полученный синдром С_{1т мод} (х) = х² является модифицированным.

2) Рассмотрим случай, когда имеется двойная смежная ошибка. Сформируем вектор ошибки:

Е₂ = 1100000; е₂ (х) = х⁶ + х⁵.

Произведем деление на производящий полином:

Полученный синдром С_2т (х) = х получился таким, как если бы в канале присутствовала независимая ошибка. Отсюда следует, что код (7, 4) не обладает способностью исправлять ошибки 2-й кратности.