В нашем случае в канале передачи информации действуют ошибки как 1-й, так и 2-й кратности (см. п. 7). В случае, если канал был бы односторонний, пришлось бы применять другое соотношение, так как нужно было бы исправлять ошибки 1-й и 2-й кратности. Однако у нас (см. п. 4) канал передачи двусторонний, что значительно снижает вероятность появления в канале передачи ошибки 2-й кратности. Поэтому исправлением ошибок 2-й кратности мы пренебрегаем; мы их только обнаруживаем, что и соответствует формуле (8).
· Важнейшим параметром кода является его производящий полином. По этому полиному производится аппаратная реализация схемы деления кодера.
Определим производящий полином g(x), исходя из того, что для соответствия выбранному коду он должен удовлетворять трем условиям:
1. Старшая степень полинома должна быть равна (n – k).
2. Деление многочлена (хn + 1) на производящий многочлен должно производиться без остатка.
3. Если код исправляет только независимые (1-й кратности) ошибки, то производящий полином должен быть неприводим (неразложим на множители).
Само определение производящего полинома производится подбором.
Проверим на соответствие этим условиям многочлен g(х) = х3 + х + 1.
Соответствие 1-му и 3-му условиям очевидно; проверим его на соответствие 2-му условию, произведя деление:
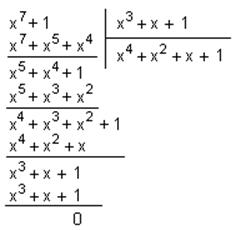
Отсюда видно, что 2-е условие тоже выполняется.
3. ПОСТРОЕНИЕ КОДЕРА В ЦИКЛИЧЕСКИЙ (n, k) КОД
Перед тем, как реализовать кодер аппаратно, промоделируем его работу математически.
Для этого возьмем произвольную комбинацию l, которую затем будем подавать на вход кодера, и закодируем ее теоретически в циклический систематический (n, k) код. Следует отметить, что число разрядов в l(x) должно равняться k, т.е. 4:
l = 1001.
Представим эту комбинацию в виде полинома:
l(х) = х3 + 1.
Умножим этот полином на множитель хn-k. Т.к. у нас формируется систематический код, то это делается для того, чтобы сдвинуть исходную кодовую комбинацию (информационные разряды кода) на (n – k) разрядов влево:
l’(х) = (х3 + 1) ∙ х7-4 = (х3 + 1) ∙ х3 = х6 + х3
Разделим полученный полином на производящий полином g(х). При этом в остатке получаем значения контрольных разрядов кода.
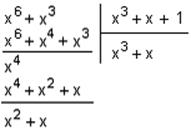
В остатке получаем полином R(х) = х2 + х.
Искомая кодовая комбинация будет состоять из двух слагаемых, первое из которых представляет собой сдвинутые информационные символы, а второе – контрольные символы:
v(х) = l’(х) + R(х) (9)
v(х) = х6 + х3 + х2 + х.
Сформируем кодовую комбинацию по кодовому полиному:
v = 1001110.
Эту кодовую комбинацию должен формировать кодер на выходе при поступлении на его вход комбинации l. При этом первые 4 разряда являются информационными, а 3 оставшиеся – контрольными (начиная со старшего разряда).
Структурная схема кодера
Структурная схема кодера представлена на рис. 3.
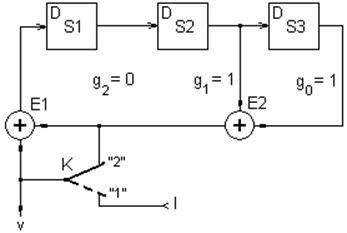
Рис. 3.
Основными элементами кодера являются:
- элементы задержки на D-триггерах S1, S2, S3;
- сумматоры по модулю два E1, E2;
- двухпозиционный ключ К.
Принцип работы схемы:
Первые k тактов (т. е. 4) ключ К находится в положении «1». Информационные разряды кода подаются от входной комбинации l непосредственно на выход v и на вход схемы деления на производящий многочлен, собранной на сумматорах и триггерах.
По прошествии k тактов ключ К перекидывается в положение «2», и оставшиеся на элементах памяти (триггерах) контрольные разряды (т.е. остаток от деления на g(x)) переходят в течение оставшихся трех тактов на выход v. При этом на выходе Е1 получаем нули (т.к. либо происходит сложение «1+1», либо «0+0»).
Принцип построения схемы деления:
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.