4.5. Проверка гипотезы о нормальном распределении параметра «Доход за год., т.руб.»
Number of valid cases:145
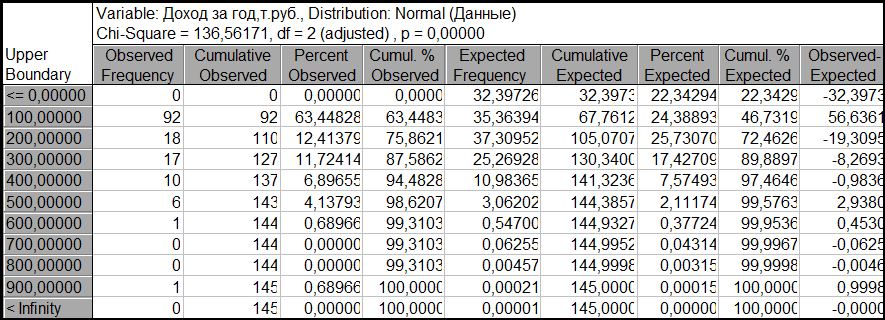
Observed mean = 112,084543, Observed variance = 21712,391688
Distribution: Normal
Parameters: Mean = 112,0845, Variance = 21712,39
Number of valid cases:145
Observed mean = 112,084543, Observed variance = 21712,391688
Distribution: Normal
Parameters: Mean = 112,0845, Variance = 21712,39
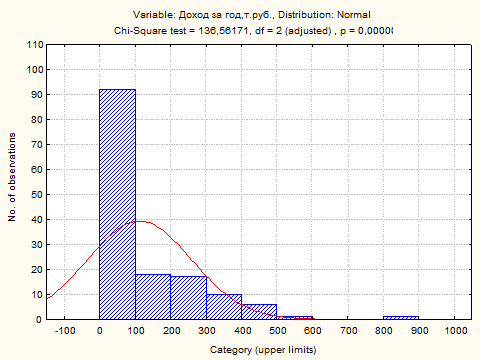
Мы видим, что вероятность функции распределения (р) = 0,0000 (бесконечно малое), таким образом, можно сделать вывод, что выдвинутая нами гипотеза о нормальном распределении – отвергается. Если посмотреть на график функции распределения по параметру «Доход за год, т.руб.», можно наглядно убедиться в опровержении гипотезы о нормальности.
§ Подгонка вида распределения
4.5.1. Гипотеза о прямоугольном виде распределения
Number of valid cases:145
Observed mean = 112,084543, Observed variance = 21712,391688
Distribution: Rectangular
Parameters: Min. range Parameter = ,9792000, Max. range Parameter = 842,4000
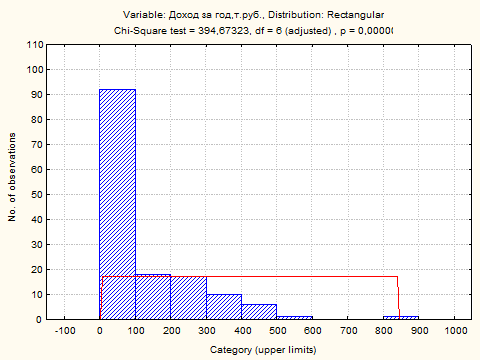
Выдвинутая гипотеза о прямоугольном виде распределения для параметра «Доход за год, т.руб.» отвергается с вероятностью Р = 0,00000
4.5.2. Гипотеза об экспоненциальном виде распределения
Number of valid cases:145
Observed mean = 112,084543, Observed variance = 21712,391688
Distribution: Exponential
Parameters: Lambda = ,8922E-2
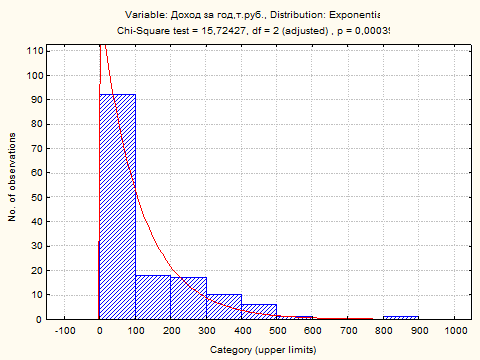
Выдвинутая гипотеза об экспоненциальном виде распределения для параметра «Доход за год, т.руб.» отвергается с вероятностью Р = 0,00039
4.5.3. Гипотеза о Гамма-распределении
Number of valid cases:145
Observed mean = 112,084543, Observed variance = 21712,391688
Distribution: Gamma
Parameters: Scale parameter = 216,4249, Shape parameter = ,5178912
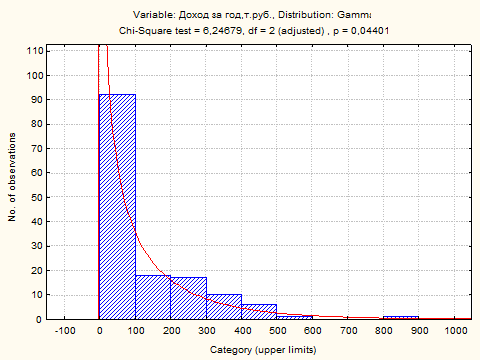
Выдвинутая гипотеза для параметра «Доход за год, т.руб.» о равенстве Гамма-распределению принимается свероятностью Р = 0,05
5. Гипотезы о равенстве математических ожиданий исследуемых переменных
5.1. Гипотеза о равенстве математических ожиданий исследуемых переменных заданным значениям с помощью одновыборочного t-теста
§ Одновыборочный t-тест для проверки гипотезы о равенстве математического ожидания значению 350 для параметра «Выпуск в мес., шт.»

Гипотеза о равенстве математического ожидания значению 350 принимается с вероятностью р=0,105
§ Одновыборочный t-тест для проверки гипотезы о равенстве математического ожидания значению 85 для параметра «Доход в год., тыс.руб.»

Гипотеза о равенстве математического ожидания значению 85 отвергается с вероятностью р=0,105
5.2. Гипотеза о равенстве математических ожиданий двух выборок с использованием двухвыборочного t-теста
§ Двухвыборочный t-тест для проверки гипотезы о равенстве математических ожиданий двух выборок «Наименование продукции» от ДГУП (филиалов) [Таким образом, выдвигается гипотеза о равенстве номенклатуры выпускаемой продукции между двумя ДГУПами {филиалами}]

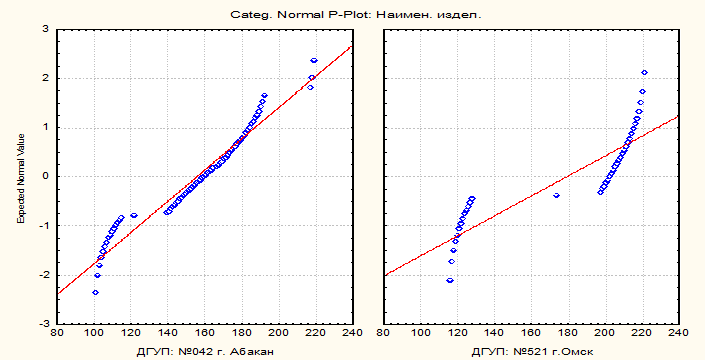
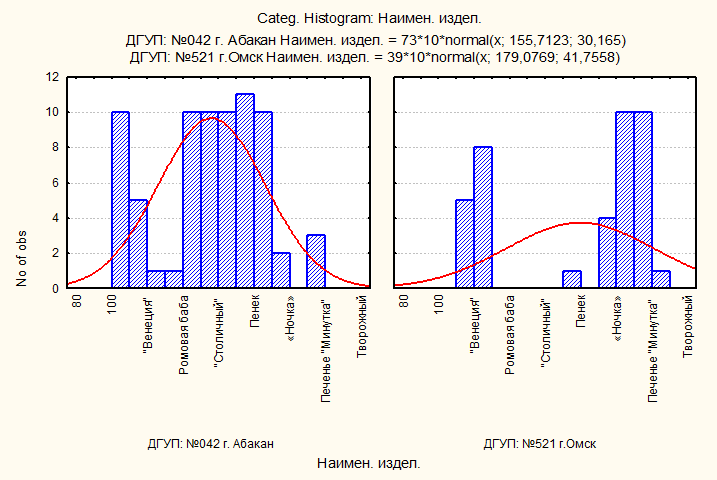
Поскольку наблюдения внутри групп не распределены нормально, использование t-критерия невозможно

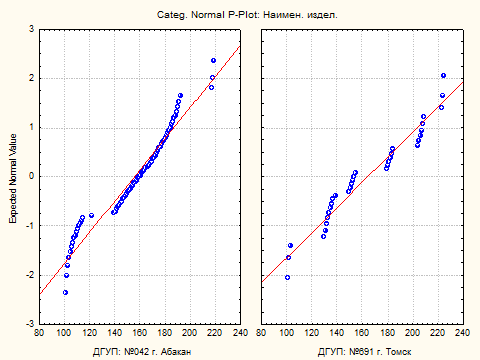
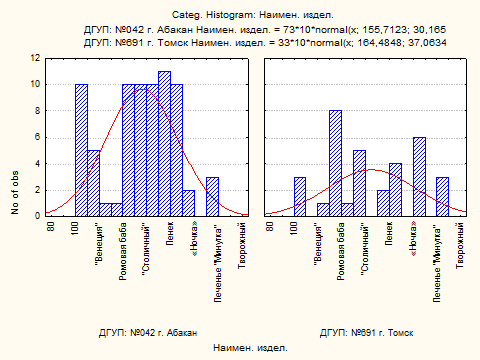
Поскольку наблюдения внутри групп не распределены нормально, использование t-критерия невозможно
6. Вычислим корреляционную матрицу для исследуемых выборок
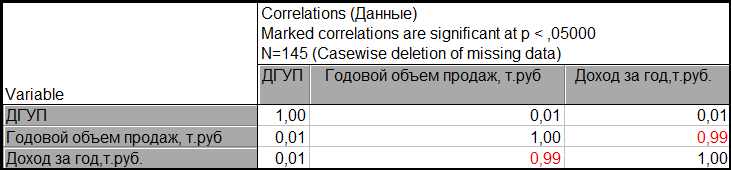
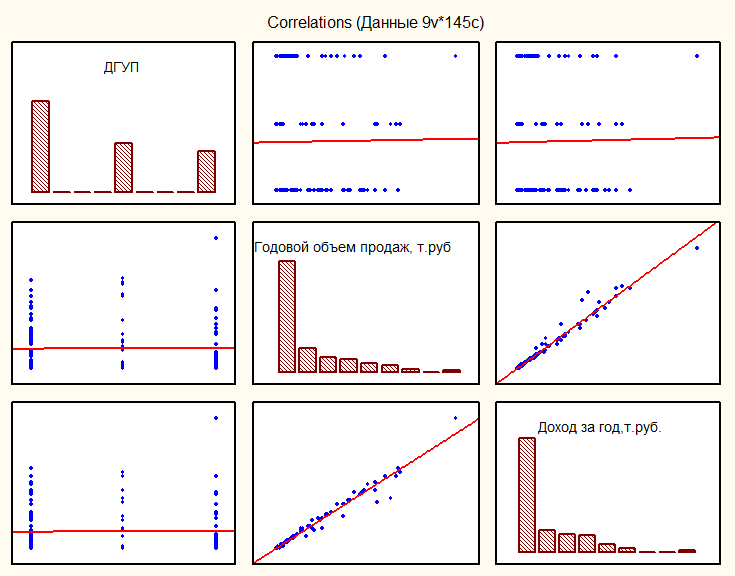
Мы наблюдаем значительную положительную корреляцию между «годовым объемом продаж, тыс. руб.» и «Доходом за год, тыс. руб.» (чем больше объем продаж, тем больше доход)
Если рассмотреть в отдельности корреляционные матрицы, то зависимость параметра «Годовой объем продаж, т.руб.» от «Доход за год, т.руб.» будет видна в явном виде:

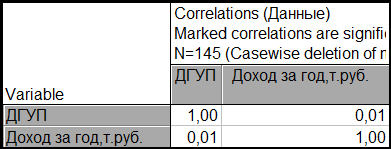
при этом «Доход за год, т.руб.» никак не зависит от филиала (ДГУП):
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.