Разведывательный анализ данных с использованием модуля Basic Statistics (Основные статистики) и Distribution Fitting (Подгонка распределений) пакета STATISTICA., страница 5

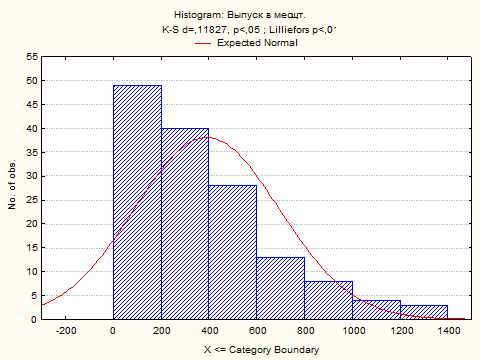
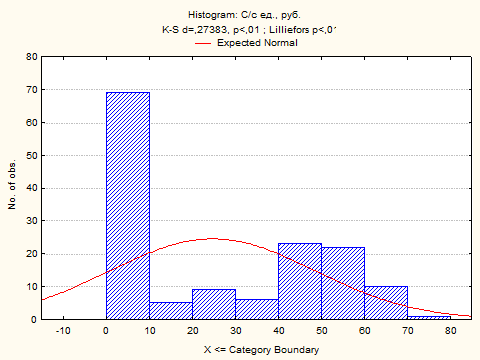
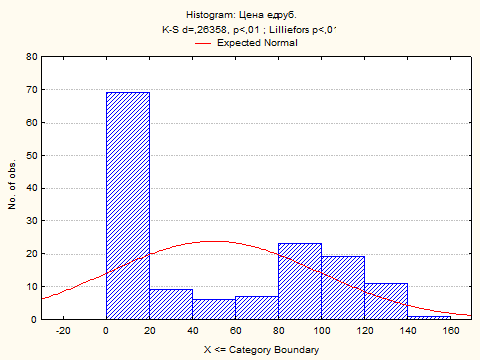
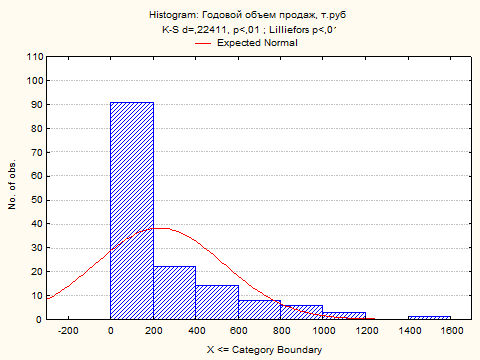
Для визуального представления полученных при помощи таблиц частот результатов, построим гистограммы для анализируемых (некатегоризованных) данных.

3.2.2. Гистограммы

Гистограмма для параметра «Выпуск в мес., шт.»  показывает динамику изменения выпуска продукции по отношению к ассортименту продукции. Чем больше выпуск, тем меньше попадает в этот интервал наблюдений.

Гистограмма для параметра «Себестоимость единицы изделия, руб.»  отображает расходы на производство изделий. Больше всего наблюдений попадает в интервал от 0 до 10 руб. («пирожные»/ «хлебобулочные изделия») Интервал от 40 до 80 – это себестоимость тортов/рулетов.

Гистограмма для параметра «Цена единицы, руб.»  показывает зависимость цены от себестоимости. Если сравнить с предыдущей гистограммой, то можно убедиться, что действительно, цена отображает себестоимость + наценку, т.о. функция распределения будет аналогичной

Гистограмма для параметра «Годовой объем продаж, т.руб.» показывает, что наибольший объем продаж наблюдается в  интервале от 0 до 200 тыс. руб. Есть также и максимальный выброс – в интервале от 1400 до 1600 тыс.руб.

Гистограмма для параметра «Доход за год, т.руб.» показывает, что наибольший доход наблюдается в  интервале от 0 до 200 тыс. руб. Если бы не максимальный выброс (интервал от 800 до 1000 тыс. руб.) можно было бы сделать предположение о нормальном распределении функции.

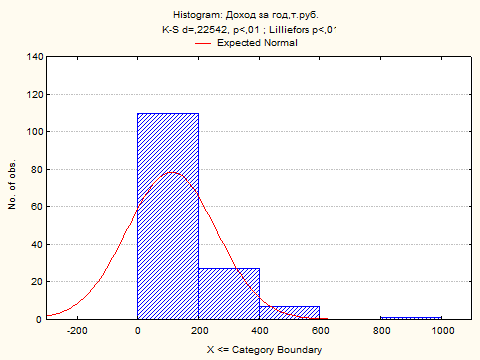
Из построенных гистограмм видно, что ни одна из функций распределений не является нормальной.

Построим диаграмму типа «Ствол с листьями» для параметра «Доход за год, тыс. руб.»

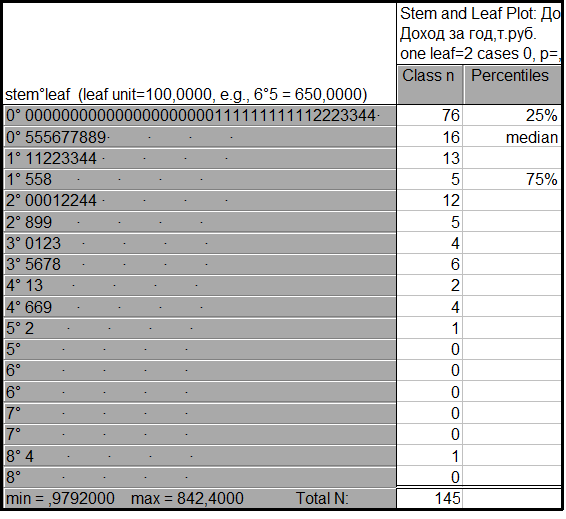
Диаграмма типа «Ствол с листьями» показывает, что минимальное значение = 0,979 тыс. руб., а максимальное значение – 842,4 тыс. руб. из общего числа наблюдений 145.

4)  Проверка гипотез о виде распределения исследуемых непрерывных и дискретных признаков    // Подгонка распределений

4.1. Проверка гипотезы о нормальном распределении параметра «Выпуск в мес., шт.»

Number of valid cases:145

Observed mean = 391,206897, Observed variance = 92267,484674

Distribution: Normal

Parameters: Mean = 391,2069, Variance = 92267,48

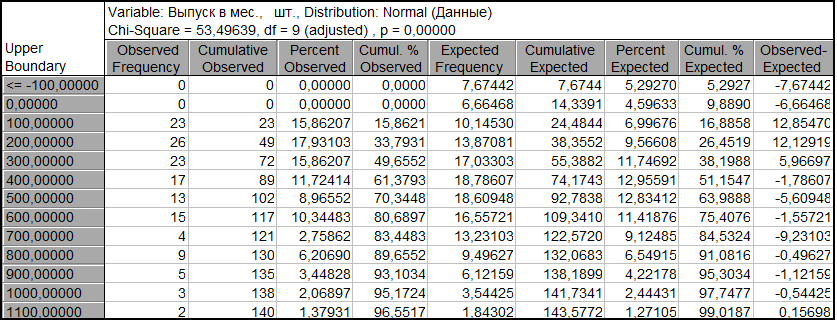
Number of valid cases:145

Observed mean = 391,206897, Observed variance = 92267,484674

Distribution: Normal

Parameters: Mean = 391,2069, Variance = 92267,48

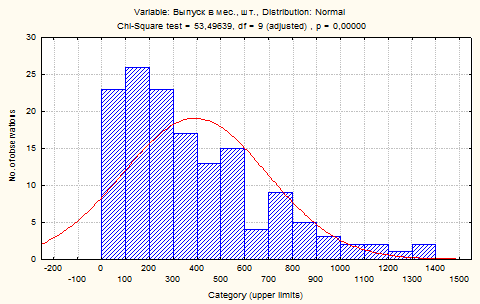
Мы видим, что вероятность функции распределения (р) = 0,0000 (бесконечно малое), таким образом, можно сделать вывод, что выдвинутая нами гипотеза о нормальном распределении – отвергается. Если посмотреть на график функции распределения по параметру «Выпуск в мес. в шт.», то можно наглядно убедиться в опровержении гипотезы о нормальности.

§  Подгонка вида распределения

4.1.1. Гипотеза о прямоугольном виде распределения

Number of valid cases:145

Observed mean = 391,206897, Observed variance = 92267,484674

Distribution: Rectangular

Parameters: Min. range Parameter = 20,00000, Max. range Parameter = 1320,000

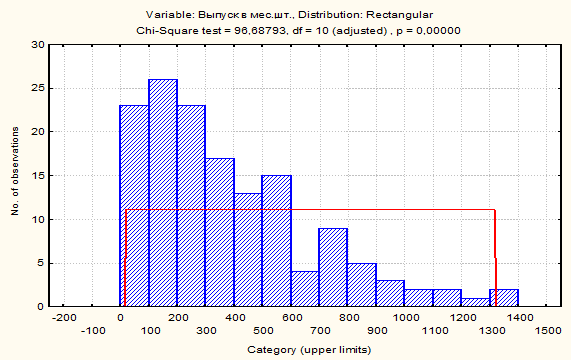
Выдвинутая гипотеза о прямоугольном виде распределения отвергается, т.к. вероятность

Р = 0,00000

4.1.2.  Гипотеза об экспоненциальном виде распределения

Number of valid cases:145

Observed mean = 391,206897, Observed variance = 92267,484674

Distribution: Exponential

Parameters: Lambda = ,2556E-2

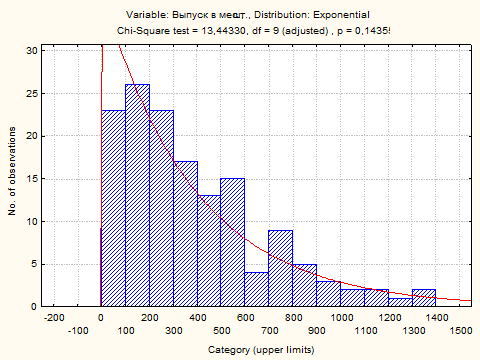
Выдвинутая гипотеза об экспоненциальном  виде распределения отвергается с  вероятностью Р = 0,143

4.1.3.  Гипотеза о Гамма-распределении