4.5.3. Пусковые токи определим через фактические значения линейных токов I!л и коэффициент пусковых токов кI=Iп/Iн =7,5: I!п = I!л · кI =125,4·7,5=940,5 А, что в I!п / Iп =940,5/313,5=3 раза превышает значение пусковых токов при подключении звездой.
4.5.4. Моменты, развиваемые
двигателем (пусковой Мп , критический Мкр )
изменяются пропорционально квадрату напряжения на фазных обмотках, т.е. М =
км U2ф . Так как напряжение на фазных обмотках при ошибочном
способе подключения двигателя (треугольником) увеличилось в
раз, моменты двигателя увеличатся в ()2 раз, т.е. в 3 раза.
При соединении фазных обмоток двигателя звездой М = км U2ф = км·2202 , откуда км =М/2202 .
При соединении обмоток двигателя треугольником М! = км (U!ф)2 =М·3802 /2202 =3М.
Пусковой момент при подключении двигателя треугольником (ошибочном способе) М!п =3Мп =3·93,7=281,1 Н·м.
Критический момент при подключении двигателя треугольником М!кр =3Мкр =3·158,6=475,8 Н·м.
4.5.5. Мощность на валу
двигателя выражается Pн=UлIл ηн
cosφн . Из величин, входящих в это выражение, при ошибочном
выборе способа подключения двигателя изменяется только линейный ток Iл (напряжение сети Uл =380 В не изменяется). Согласно результату расчёта п. 4.5.2.
при ошибочном подключении двигателя треугольником токи линейные увеличиваются в
3 раза, следовательно, и мощность двигателя при номинальном скольжении
увеличится в 3 раза и составит P!н =3Pн =3·22=66 кВт.
5. Рассчитать время tпуск и построить кривую разгона электропривода n(t).
Процессы, связанные с изменением моментов (двигателя М и рабочей машины Мс ) и скорости ω электропривода, описываются уравнением движения привода
М – Мс =J·dω/dt, (13)
где ω – угловая скорость вала двигателя, 1/с; М – момент, развиваемый двигателем, Н·м;
Мс – момент статического сопротивления рабочей машины (нагрузки), приведённый к валу двигателя, Н·м; J – момент инерции системы, приведённый к валу двигателя, кг·м2.
Момент статического сопротивления рабочей машины Мсм приводится к валу двигателя по выражению (1).
Кинетическая энергия системы определяется как сумма кинетических энергий всех валов и подвижных частей системы:
Jд ω2д /2+ J1 ω21 /2+…+ Ji ω2i /2+…+ Jn ω2n /2= J ω2д /2, (14)
где Jд, J i – моменты инерции вала двигателя и отдельных i-х валов машины, соответственно, кг·м2;
ωд, ωi – угловая скорость вала двигателя и i-х валов машины, соответственно, 1/с.
Момент инерции системы J, приведённый к валу двигателя, определяется из выражения (14):
J=Jд+J1(ω1/ ωд )2+…+ J i (ωi / ωд)2. (15)
Разность моментов (М – Мс) называют динамическим моментом Мдин, под действием которого электропривод ускоряется или замедляется.
Поскольку на практике скорость вращения двигателя и рабочей машины обычно оценивается не в единицах СИ, а во внесистемных единицах (частота вращения n, об/мин), выразим угловую скорость ω через частоту вращения вала n: ω=π n/30 = n/9,55. Тогда уравнение движения привода будет иметь вид: М – Мс =(1/9,55)J·dn/dt (14)
Из уравнения (14) выразим бесконечно малое приращение времени
dt=(1/9,55) J·dn/(М – Мс) (15)
Проинтегрировав уравнение (15) в пределах изменения n, получим время переходного процесса t, за которое система «электродвигатель – рабочая машина»
(электропривод) перейдёт от одного установившегося режима к другому: t1-2=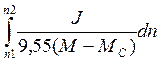
(16).
Решение уравнения (16) не вызывает затруднений при условии, что момент инерции J, моменты М и Мс не зависят от скорости, т.е. (М – Мс)=const и J=const. Однако статические моменты М и Мс асинхронных двигателей и рабочих машин обычно имеют сложную зависимость от скорости или описываются эмпирическими зависимостями, поэтому аналитический расчёт переходных процессов электропривода оказывается затруднённым.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.