Анализ устойчивости и качества процесса управления в линейной непрерывной САУ, страница 3

При подготовке к выполнению данного пункта рекомендуется следующий материал: [1] – C. 146 – 157; [2] – C. 186 – 200; [3] – C. 228 – 233; [4] – C. 162 – 174; [6] – C. 74 – 81.

Установившийся режим – это такой режим, при котором ошибка системы постоянна во времени.

Точность системы автоматического регулирования (САР) в установившемся режиме определяется величиной установившейся ошибки .

Точность САР рассматривают по отношению к следующим типовым установившимся режимам:

а) неподвижному состоянию (статический режим), характерному для систем стабилизации регулируемых координат, для которого ;

б) движению с постоянной скоростью (динамический режим), характерному для следящих систем с астатизмом , для которого ;

в) движению с постоянным ускорением (динамический режим), характерному для следящих систем с астатизмом , для которого .

Типовому движению «а» соответствует статическая (позиционная) установившаяся ошибка , если ; движению «б» – динамическая (кинетическая) установившаяся ошибка по скорости , (, так как ); движению «в» – динамическая установившаяся ошибка по ускорению  (, так как ).

Поскольку САР находится под влиянием как задающего, так и возмущающего сигналов, то в ней будет возникать суммарная установившаяся ошибка .

В контрольной работе необходимо вычислить суммарную установившуюся ошибку системы. Наиболее удобными математическими моделями для расчета  являются передаточные функции  и , представленные после преобразования в виде (2.2) и (2.3).

В выражениях (2.2) и (2.3) подразумевается, что

,                                          (2.16)

где  – степень сомножителя , связанного со свободными членами полиномов  и соответственно .

Из (2.16) следует, что порядок астатизма системы по заданию (возмущению) равен , т. е.

.                                                (2.17)

В зависимости от точки приложения возмущения

.                                                       (2.18)

В таблице 1.2 функции  и  содержат одно или несколько типовых движений, по отношению к которым необходимо определить . Так, например, если , то в нем присутствуют все типовые движения с параметрами: ; .

Суммарную установившуюся ошибку можно определить двумя способами:

-  по теореме операционного исчисления о конечном значении оригинала

,     (2.19)

где  и  – изображение по Лапласу функций  и ;

-  по методу коэффициентов ошибок

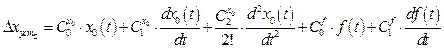,  (2.20)

если, например, , а .

Наиболее простым методом нахождения коэффициентов ошибок по заданию () и возмущению () является разложение передаточных функций  (соответственно ) в степенной ряд путем деления многочлена числителя передаточных функций на знаменатель, выставив предварительно (перед делением) полиномы числителя и знаменателя по возрастающим степеням.

2.4 Методические указания к выполнению пункта 1.3.4 программы контрольной работы

При подготовке к выполнению данного пункта рекомендуется материал: [1] – C. 195 – 208; [2] – C. 200 – 214; [3] – C. 193 – 224; [5] – C. 17 – 26; [6] – C.82 – 84.

Переходный режим – это переход системы из одного установившегося состояния в другое под действием приложенного возмущения, либо вследствие ненулевых начальных условий.

Точность системы в переходном режиме определяется величиной переходной ошибки, т. е. величиной отклонения управляемой координаты  от заданного значения  и длительностью существования этих отклонений.

Точность системы в переходном режиме оценивается с помощью прямых и косвенных методов.

Прямые методы – это методы расчета на современных ЭВМ переходной характеристики , являющейся реакцией системы на самое «тяжелое» воздействие – единичное ступенчатое, по которой непосредственно (прямо) оценивается качество управления в переходном режиме.

Среди прямых показателей качества переходного процесса важнейшими являются:

-  максимальное перерегулирование ;

-  время регулирования .

Однако чаще всего целесообразнее для предварительной оценки качества переходного процесса воспользоваться либо косвенными методами, базирующимися на использовании частотных характеристик и справедливыми для минимально-фазовых систем, либо приближенными методами расчета , не прибегая к компьютерам. Одним из таких простых методов является метод трапеций, предложенный В. В. Солодовниковым и А. А. Вороновым и доступно изложенный в [8] – C. 112 – 119.

При отсутствии ЭВМ воспользуйтесь [8].

Для предварительной оценки качества переходного процесса рекомендуются следующие частотные характеристики:

-  ЛАЧХ () и ЛФЧХ () разомкнутой системы;

-  АЧХ () – амплитудно-частотная характеристика замкнутой системы;

-  ВЧХ () – вещественная частотная характеристика замкнутой системы.

По  и  находят запасы устойчивости по модулю , по фазе  и частоту среза, по численным значениям которых приближенно судят о величинах  и  в замкнутой системе.

Удовлетворительным по качеству считается переходный процесс, у которого = 6 ÷ 20 дБ, = 30 ÷ 60 градусов, а  как можно больше, так как .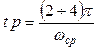

По  по каналу  оценивают частотный показатель колебательности  по формуле

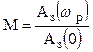,                                               (2.21)

где  – значение  на резонансной частоте ;

 – начальное значение .

Чем больше отношение (2.21), тем больше перерегулирование  (тем сильнее колебательность системы) и, как следствие, больше длительность регулирования .

Косвенными частотными показателями быстродействия системы служат: резонансная частота  и частота незатухающих колебаний .

С учетом гипотезы эквивалентности динамических свойств замкнутой системы регулирования свойствам колебательного звена второго порядка (см. С. 206 – 208 в [1]) для практических задач в диапазоне реальных значений , которым соответствуют , рекомендуются для определения прямых показателей качества переходного процесса  и  следующие простые выражения:

.                                (2.22)