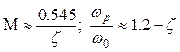 , (2.23)
, (2.23)
где ![]() – коэффициент демпфирования;
– коэффициент демпфирования;
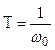 –
период незатухающих колебаний.
–
период незатухающих колебаний.
Значения ![]() и Т определяются
из (2.23) через М и
и Т определяются
из (2.23) через М и ![]() и подставляются в (2.22)
для нахождения приближенных значений
и подставляются в (2.22)
для нахождения приближенных значений ![]() и
и ![]() .
.
Амплитудно-частотная характеристика замкнутой
системы ![]() рассчитывается и строится по
рассчитывается и строится по ![]() (см. выражение 2.1), которое, после
подстановки
(см. выражение 2.1), которое, после
подстановки ![]() преобразуется в (2.24).
преобразуется в (2.24).
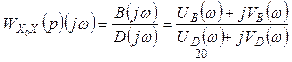 . (2.24)
. (2.24)
Из выражения (2.24) находим ![]()
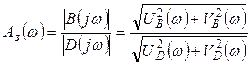 . (2.25)
. (2.25)
По ![]() по каналу
по каналу ![]() определяют
определяют ![]() и
оценивают перерегулирование
и
оценивают перерегулирование ![]() по формуле
по формуле
![]() . (2.26)
. (2.26)
Косвенным частотным показателем быстродействия на
характеристике ![]() служит частота интервала
положительности
служит частота интервала
положительности ![]() вещественной частотной
характеристики замкнутой системы, которая с частотой среза
вещественной частотной
характеристики замкнутой системы, которая с частотой среза ![]() ЛАЧХ разомкнутой системы связана
следующим соотношением
ЛАЧХ разомкнутой системы связана
следующим соотношением
![]() .
(2.27)
.
(2.27)
Тогда приближенно
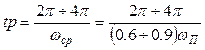 . (2.28)
. (2.28)
ВЧХ замкнутой системы рассчитывается по передаточной
функции ![]() в соответствии с методикой,
рассмотренной в пункте 2.2.
в соответствии с методикой,
рассмотренной в пункте 2.2.
Для выделения ![]() из
из
![]() необходимо
необходимо ![]() представить
следующим образом
представить
следующим образом
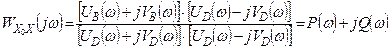 ,
(2.29)
,
(2.29)
где ![]() –
вещественная часть
–
вещественная часть ![]() ;
;
![]() –
мнимая часть
–
мнимая часть ![]() .
.
После несложных преобразований получаем выражение
для расчета ![]()
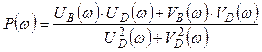 . (2.30)
. (2.30)
При выполнении пункта 1.3.4 программы контрольной работы студент может самостоятельно выбрать любой из предложенных методов для оценки точности управления в переходном режиме. Однако предпочтительнее использовать прямой метод, например, метод структурного моделирования на ЭВМ, так как структурная схема замкнутой системы уже задана (см. таблицу 1.1) и является достаточно простой для моделирования.
Оценка качества процесса управления осуществляется по следующим показателям:
- запасам устойчивости;
- установившейся ошибке;
- максимальному перерегулированию и времени регулирования.
Если заказчик, т. е. преподаватель, конкретно не указал требуемые числовые значения этих показателей, то они должны удовлетворять общепринятым минимально или максимально-допустимым значениям, обеспечивающим нормальное функционирование системы и возможность её длительной эксплуатации.
Минимально-допустимые запасы устойчивости:
![]() .
.
Точность статической системы считается
удовлетворительной, если коэффициент статизма ![]() что
соответствует
что
соответствует ![]() [1] – C.
147 – 148,
[1] – C.
147 – 148,
![]() ,
(2.31)
,
(2.31)
где ![]() – передаточный коэффициент
разомкнутого контура статической системы.
– передаточный коэффициент
разомкнутого контура статической системы.
Точность системы в динамических установившихся
режимах воспроизведения внешних воздействий ![]() и
и
![]() тем выше, чем больше
тем выше, чем больше ![]() и чем меньше параметры
воспроизведения внешних воздействий U и a. Будем считать, что точность динамической системы воспроизведения
удовлетворительна, если
и чем меньше параметры
воспроизведения внешних воздействий U и a. Будем считать, что точность динамической системы воспроизведения
удовлетворительна, если ![]() .
.
Основные показатели качества переходного режима
должны находиться в следующих пределах: ![]() ;
;
![]() .
.
Если расчетные значения показателей качества процесса управления выходят за рекомендуемые минимально или максимально допустимые пределы, то после анализа системы необходимо наметить пути синтеза дополнительных устройств, которые называются корректирующими и с помощью которых можно улучшить качество процесса управления.
При выполнении этого пункта необходимо руководствоваться следующим материалом: [1] – C. 234 – 262; [2] – C. 247 – 260; [3] – C. 234 – 253; [5] – C. 34 – 37; [9] – C. 3 – 20.
Синтез корректирующего устройства проводить не нужно, достаточно только выбрать и обосновать тот или иной путь улучшения качества процесса управления.
Контрольная работа должна быть оформлена в соответствии с [7] – С. 10 – 19 и удовлетворять требованиям межгосударственного стандарта 2.105 – 95 ЕСКД и других ГОСТ-ов.
1. Лукас В. А. Теория автоматического управления: Учеб. для вузов. – 2-е изд., перераб. и доп. – М.: Недра, 1990. – 416 с.
2. Теория автоматического управления. / Под ред. А. В. Нетушила. – М.: Высш. шк., 1976. – 400 с.
3. Попович М. Г., Ковальчук О. В. Теорія автоматичного керування. – К.: Либідь, 1997. – 554 с.
4. Сборник задач по теории автоматического регулирования и управления. / Под ред. В. А. Бесекерского. – М.: Недра, 1978. – 512 с.
5. Методические указания к домашним заданиям по курсу "Теория автоматического управления.”/Сост.: Н. Н. Сергиенко – Алчевск: ДГМИ, 2003. – 54 с.
6. Методичні вказівки до практичних занять з курсу "Теорія автоматичного керування". Частина 1. / Укл.: М. М. Сергієчко. Алчевськ: ДГМІ, 2004 – 87 с.
7. Методические указания к выполнению практических работ по курсу "Оформление технической документации" для студентов специальности 7. 092203 дневной и заочной форм обучения. / Сост. Полилов Е. В. – Алчевск: ДГМИ, 2002. – 34 с.
8. Зайцев Г. Ф. Теория автоматического управления и регулирования. – К.: Вища шк., 1988 – 430 с.
9. Теорія автоматичного керування: Практикум – 4.2 / Укл. М. М. Сергієнко. – Алчевськ: ДонДту, 2005 – 79 с.
А.1 Пример выполнения контрольной работы
А.1.1 Исходные данные
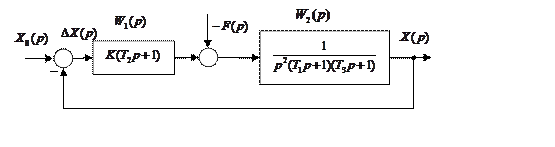
Рисунок А1.1 – Структурная схема
где
![]() =50;
=50;
![]()
![]()
![]()
![]()
![]() ; Критерий
устойчивости – Раусса
; Критерий
устойчивости – Раусса
А.1.2 Определение передаточных функций
А.1.2.1Главная передаточная функция системы
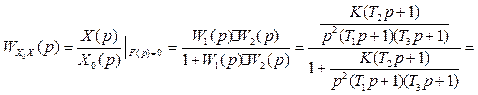
=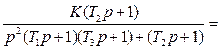
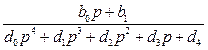 ,
,
(А1.1)
где 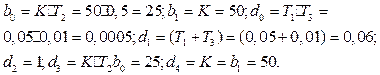 .
.
А.1.2.2 Передаточная функция по ошибке относительнозадающего воздействия ![]()
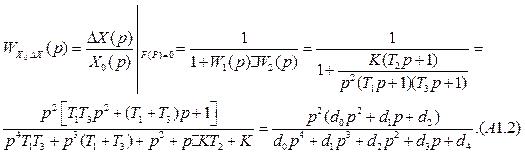
А.1.2.3
Передаточная функция по ошибке относительно возмущающего воздействия ![]()
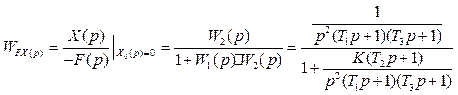 =
=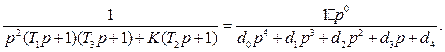 (
(![]() )
)
А.1.2.4 Передаточная функция разомкнутой системы
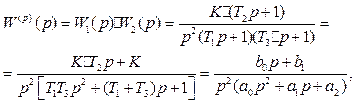 (А.1.4)
(А.1.4)
где
![]()
А.1.3 Проверка системы на устойчивость
по критерию Раусса
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.