Анализ устойчивости и качества процесса управления в линейной непрерывной САУ, страница 2

              Таблица 1.2 – Характер изменения внешних воздействий

 2 методические указания

2.1 Методические указания к выполнению пункта 1.3.1 программы контрольной работы

При подготовке к выполнению данного пункта контрольной работы рекомендуется использовать следующий материал: [1] – C. 141 – 144; [3] – C. 116 – 118; [5] – C. 26 – 30; [6] – C. 25 – 30.

Под структурной алгоритмической схемой системы подразумевается графическое изображение математической модели системы в виде совокупности передаточных функций с указанием, с помощью стрелок, связей между ними.

Структурные алгоритмические схемы широко используются в курсе ТАУ при исследовании и проектировании динамических систем. Большим достоинством структурных схем является их наглядность. По ним легко прослеживается прохождение сигналов в системе, связи между звеньями системы, влияние динамических звеньев на качество процесса управления.

По структурной схеме можно непосредственно с помощью ЭВМ провести математическое моделирование системы, используя современные программы, например Mathlab и её библиотеку блоков, находящихся в меню Sumulink и получить все необходимые частотные и временные характеристики системы.

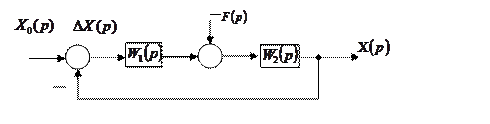
В упрощенном варианте структурную схему системы регулирования можно представить в таком виде

Рисунок 2.1 – Структурная алгоритмическая схема

Из схемы рисунка 2.1 определяем эквивалентные передаточные функции замкнутой и разомкнутой системы.

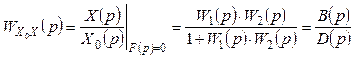,               (2.1)

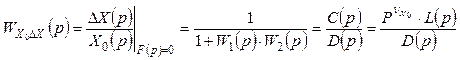, (2.2)

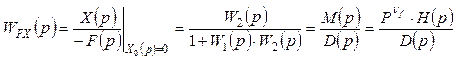, (2.3)

,                                (2.4)

где  и  – полиномы некоторой степени, получившиеся в результате преобразования выражений, записанных для эквивалентных передаточных функций;

 и  – порядок астатизма замкнутой системы соответственно по заданию  и возмущению .

Передаточную функцию  можно получить также из выражения:

,                            (2.5)

а  из выражения (2.4)

,                                    (2.6)

где  – характеристическое уравнение замкнутой системы, которое широко используется при анализе устойчивости систем.

2.2 Методические указания к выполнению пункта 1.3.2 программы контрольной работы

При подготовке к выполнению данного пункта рекомендуется использовать материал: [1] – C. 159 – 178; [2] – C. 143 – 162; [3] – C. 140 – 162, C. 171 – 183; [4] – C. 86 – 106; [6] – C. 54 – 72.

Устойчивость – это необходимое, но недостаточное условие нормального функционирования системы автоматического регулирования. Достаточным условием в устойчивой системе является обеспечение требуемого качества процесса управления.

Под устойчивостью подразумевается способность системы возвращаться в исходное состояние после исчезновения внешних сил, которые вывели её из этого состояния.

В источниках [1, 2, 3] излагаются теоретические основы теории устойчивости технических систем, даётся математическое определение понятия «устойчивости», приводятся методы анализа и исследования устойчивости.

Проверить систему на устойчивость можно с помощью различных методов, но в инженерной практике наиболее распространёнными являются критерии устойчивости, т. е. некоторые правила, которые позволяют судить об устойчивости (неустойчивости) системы без вычисления корней характеристического уравнения  замкнутой системы.

При теоретической подготовке следует изучить все рекомендуемые в таблице 1.1 критерии устойчивости, но в контрольной работе используйте только тот, который предложен для вашего варианта.

В [4] и [6] приведены решенные задачи на определение устойчивости замкнутой системы с помощью различных критериев устойчивости. Тщательно ознакомьтесь с методологией решения этих задач. Это поможет вам более качественно выполнить пункт 1.2.3 контрольной работы.

Помните, что при применении критериев Раусса, Гурвица и Михайлова для оценки устойчивости замкнутой системы используется характеристическое уравнение (2.6) замкнутой системы, которое получено в 1.3.1.

При применении критерия Найквиста об устойчивости замкнутой системы судят по виду амплитудно-фазовой характеристики (АФХ) или по виду логарифмических амплитудно и фазо-частотных характеристик (ЛАЧХ и ЛФЧХ) разомкнутой системы. Для их построения используется передаточная (2.4) функция разомкнутой системы, т. е. .

АФХ разомкнутой системы строится следующим образом. В выражении (2.4) подставляется . Тогда

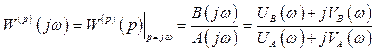,         (2.7)

где ,  – действительная и мнимая части комплексного выражения ;

,  – действительная и мнимая части комплексного выражения .

Избавляются от иррациональности в знаменателе выражения (2.7) путем умножения числителя и знаменателя комплексной передаточной функции  на комплексно-сопряженное знаменателю выражение . Тогда выражение (2.7) примет вид

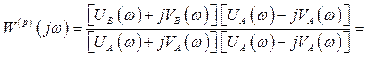
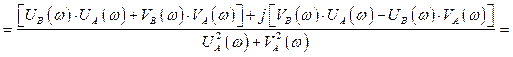
                                         (2.8)

         где

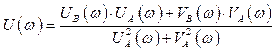,                  (2.9)

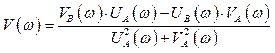.              (2.10)

АФХ строят по точкам, изменяя частоту от  до . Количество точек между частотами  и  должно быть достаточным для определения вида амплитудно-фазовой характеристики.

Для построения по точкам ЛАЧХ, т. е. , можно воспользоваться следующими выражениями:

 дБ,                             (2.11)

где согласно (2.8)

                        (2.12)

или согласно (2.7)

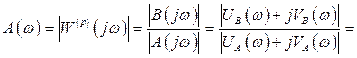
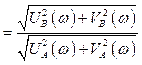.                                 (2.13)

Подставляя (2.12) или (2.13) в (2.11), получим уравнение для построения логарифмической амплитудно-частотной характеристики .

Для построения логарифмической фазо-частотной характеристики (ЛФЧХ), т. е. , можно воспользоваться следующими выражениями:

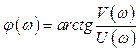                                  (2.14)

или

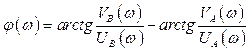                      (2.15)

Для расчета и построения АФХ,  и  рекомендуется использовать вычислительную технику и соответствующие программы.

2.3 Методические указания к выполнению пункта 1.3.3 программы контрольной работы