Общий КПД трехступенчатого редуктора:
η1h = η12
∙ η23
∙![]() =
0,962 ∙ 0,93 = 0,86.
=
0,962 ∙ 0,93 = 0,86.
Г) Зубчатый редуктор с эпигипоциклическим механизмом (рис. 7.15).
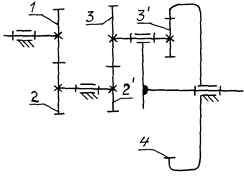
Механизм имеет две ступени: простую z1/z2 и эпигипоциклический планетарный механизм. Его КПД определяют по формуле (7.30), передаточное отношение – по формуле (7.10).
Пример 7.6. Рассчитать передаточное отношение, угловую скорость
выходного звена, общий КПД зубчатого
редуктора с эпигипоциклическим механизмом
по следующим исходным данным: числа зубьев колёс: z1 = 23; z2 = 79; ![]() = 18; z3 = 56;
= 18; z3 = 56; ![]() = 22; z4 = 96; КПД одной
ступени η = 0,96. Угловая скорость ведущего звена ω1 =
- 300 с-1.
= 22; z4 = 96; КПД одной
ступени η = 0,96. Угловая скорость ведущего звена ω1 =
- 300 с-1.
Решение.
Передаточные отношения ступеней: i12 = - z2/z1 = - 79/23 = - 3,43; 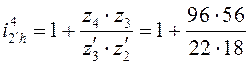 = 14,58.
= 14,58.
Общее передаточное отношение: i1h = - 3,43 ∙ 14,58 = - 50,1.
Угловая скорость выходного звена ωh = - 300/(- 50,1) = 6 с-1 (звенья 1 и h вращаются в разные стороны).
КПД планетарной передачи – формула (7.30):
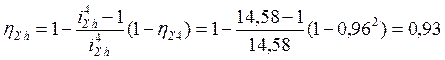 .
.
Общий КПД двухступенчатого
редуктора: η1h =
η12
∙ ![]() =
0,96 ∙ 0,93 = 0,89.
=
0,96 ∙ 0,93 = 0,89.
Д) Зубчатый механизм с редуктором Давида (рис. 7.16).
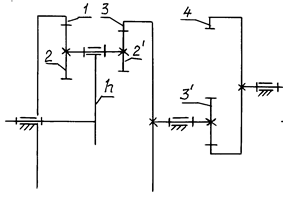
В двухступенчатом
редукторе все зацепления внутренние: планетарная и простая ![]() /z4. КПД редуктора Давида при
/z4. КПД редуктора Давида при ![]() > 0:
> 0:
|
|
(7.31) |
при ![]() < 0
< 0
|
|
(7.32) |
Передаточное отношение редуктора Давида:
 .
.
Пример 7.7. Рассчитать передаточное отношение, угловую скорость
выходного звена, общий КПД зубчатого механизма с редуктором Давида по следующим
исходным данным: числа зубьев колёс: z1 = 150; z2 = 32; ![]() = 31; z3 = 151;
= 31; z3 = 151; ![]() = 22; z4 = 140; КПД одной ступени η = 0,95. Угловая скорость
водила h ωh = 250 с-1.
= 22; z4 = 140; КПД одной ступени η = 0,95. Угловая скорость
водила h ωh = 250 с-1.
Решение.
Передаточные
отношения ступеней: 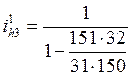 = - 25,55;
= - 25,55;
![]() = z4/
= z4/![]() = 140/22
= 6,63.
= 140/22
= 6,63.
Общее передаточное
отношение: ih4 = ![]() = - 25,55 ∙ 6,63 = - 169,4.
= - 25,55 ∙ 6,63 = - 169,4.
Угловая скорость выходного колеса ω4 = 250/(- 169,4) = - 1,48 с-1 (звенья h и 4 вращаются в разные стороны).
КПД планетарной передачи – формула (7.32):
 = 0,28.
= 0,28.
Общий КПД двухступенчатого редуктора:
![]() .
.
Е) Зубчатый механизм с планетарным редуктором типа 3k (рис. 7.17).
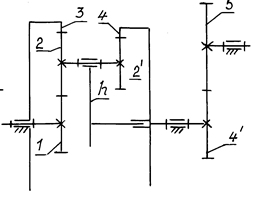
Передаточное отношение планетарного редуктора определяют по формуле (7.12):
|
|
КПД планетарного редуктора так же, как и передаточное отношение, определяют произведением КПД двух элементов передачи:
|
Пример 7.8. Рассчитать передаточное отношение, угловую
скорость выходного колеса и общий КПД зубчатого механизма с планетарным
редуктором типа 3k по следующим исходным данным: числа зубьев
колёс: z1 =
18; z2 =
41; Решение. Передаточное отношение планетарной передачи: Передаточное отношение простой зубчатой передачи: Общее передаточное отношение: i15 = |
Передаточное отношение первого элемента планетарной передачи – формула (7.9):
![]() .
.
КПД первого элемента планетарной передачи – формула
(7.30): 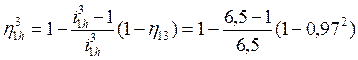 = 0,95.
= 0,95.
Передаточное отношение второго элемента планетарной передачи – формула (7.11):
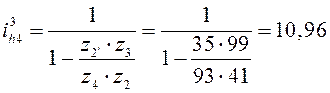 .
.
КПД второго элемента – формула (7.31): 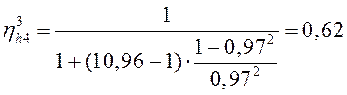 .
.
КПД планетарного редуктора: η14 = 0,95 ∙ 0,62 = 0,58.
Общий КПД
двухступенчатого редуктора: η15
= η14 ∙ ![]() = 0,58 ∙ 0,97 = 0,57.
= 0,58 ∙ 0,97 = 0,57.
Угловая скорость ведомого звена:
ω5 = ω1/i15 = 200/( - 363,8) = - 0,55 с-1.
Передаточное отношение первого элемента планетарной передачи – формула (7.9):
![]() .
.
КПД первого элемента планетарной передачи – формула
(7.30): 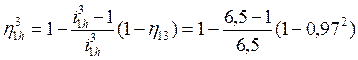 = 0,95.
= 0,95.
Передаточное отношение второго элемента планетарной передачи – формула (7.11):
 .
.
КПД второго элемента – формула (7.31): 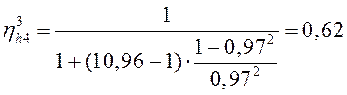 .
.
КПД планетарного редуктора: η14 = 0,95 ∙ 0,62 = 0,58.
Общий КПД
двухступенчатого редуктора: η15
= η14 ∙ ![]() =
=
0,58 ∙ 0,97 = 0,57.
Угловая скорость ведомого звена:
ω5 = ω1/i15 = 200/( - 363,8) = - 0,55 с-1.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.