1. В чём состоит цель работы?
2. Как определяется передаточное отношение зубчатого механизма?
3. Как определяется передаточное отношение многоступенчатого зубчатого механизма?
4. Назовите звенья планетарного механизма.
5. Как определяется передаточное отношение планетарного механизма?
6. Что такое обращённый механизм?
7. В чём заключается условие соосности в планетарных механизмах?
8. В чём заключается условие соседства в планетарных механизмах?
9. В чём заключается условие сборки в планетарных механизмах?
10.В чём заключается условие правильности внутреннего зацепления?
Определение передаточных отношений и механических коэффициентов полезного действия является распространенной задачей при изучении механизмов грузоподъёмных, строительных и путевых машин.
А) Трехступенчатый коническо-цилиндрический зубчатый редуктор (рис. 7.12).
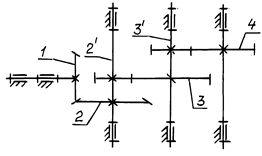
Рис. 7.12. Коническо-цилиндрический редуктор
Расчётные формулы.
Передаточные отношения ступеней: i12 = z2/z1; i23 = z3/z2 ́; i34 = z4/z3 ́.
Общее передаточное отношение: i14 = i12 ∙ i23 ∙ i34.
Общий КПД редуктора: η14 = η3.
Угловая скорость выходного звена ω4 = ω1/ i14.
Пример 7.3. Рассчитать передаточное отношение, угловую скорость
выходного колеса и общий КПД трехступенчатого коническо-цилиндрического
редуктора по следующим исходным данным: числа зубьев колёс: z1 = 24; z2 = 52; ![]() = 27; z3 = 80;
= 27; z3 = 80; ![]() = 30; z4 = 90; КПД одной ступени η
= 0,95. Угловая скорость ведущего звена ω1 = 50 с-1.
Знак передаточного отношения не учитывать.
= 30; z4 = 90; КПД одной ступени η
= 0,95. Угловая скорость ведущего звена ω1 = 50 с-1.
Знак передаточного отношения не учитывать.
Решение.
Передаточные отношения ступеней: i12 = 52/24 = 2,17; i23 = 80/27 = 2,96; i34 = 90/30 = 3.
Общее передаточное отношение: i14 = 2,17 ∙ 2,96 ∙ 3 = 19,27.
Угловая скорость выходного звена ω4 = 50/19,27 = 2,59 с-1.
Общий КПД редуктора: η14 = 0,953 = 0,86.
Б) Червячно-зубчатый редуктор (рис. 7.13).
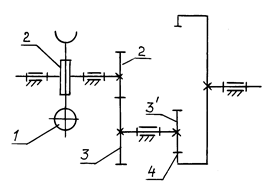
Рис. 7.13. Червячно-зубчатый редуктор
Расчётные формулы.
Передаточное отношение червячной передачи
i12 = z2/z1, где z1 – число заходов червяка.
Общий КПД трехступенчатого редуктора:
η14 = η12 ∙ η2, где η12 – КПД червячного редуктора.
Пример 7.4. Рассчитать передаточное отношение, угловую скорость
выходного колеса и общий КПД червячно-зубчатого редуктора по следующим исходным
данным: число заходов червяка z1 = 1; числа зубьев колёс: z1 = 1; z2 = 44; ![]() = 20; z3 = 84;
= 20; z3 = 84; ![]() = 24; z4 = 100; КПД червячной передачи η12 =
0,75; КПД одной зубчатой ступени η = 0,96. Угловая скорость ведущего
звена ω1 = 1000 с-1. Знак передаточного отношения
не учитывать.
= 24; z4 = 100; КПД червячной передачи η12 =
0,75; КПД одной зубчатой ступени η = 0,96. Угловая скорость ведущего
звена ω1 = 1000 с-1. Знак передаточного отношения
не учитывать.
Решение.
Передаточное отношение червячной передачи: i12 = 44/1 = 44.
Передаточные отношения ступеней: i23 = 84/20 = 4,2; i34 = 100/24 = 4,17.
Общее передаточное отношение: i14 = 44 ∙ 4,2 ∙ 4,17 = 770,62.
Угловая скорость выходного звена ω4 = 1000/770,62 = 1,3 с-1.
Общий КПД трехступенчатого редуктора: η14 = 0,75 ∙ 0,962 = 0,69.
В) Зубчатый механизм с редуктором Джеймса (рис. 7.14).

Механизм имеет три
ступени: зубчатая передача внешнего зацепления z1/z2,
зубчатая передача внутреннего зацепления ![]() и
планетарная. КПД планетарной передачи:
и
планетарная. КПД планетарной передачи:
|
|
(7.30) |
где ![]() -
КПД обращенного механизма (с неподвижным водилом), состоящего из двух зацеплений
z3 ́/z4 и z4/z5.
-
КПД обращенного механизма (с неподвижным водилом), состоящего из двух зацеплений
z3 ́/z4 и z4/z5.
Пример 7.5. Рассчитать передаточное отношение, угловую скорость
выходного звена и общий КПД зубчатого механизма с редуктором Джеймса по
следующим исходным данным: числа зубьев колёс: z1 = 19; z2 = 83; ![]() = 21; z3 = 91;
= 21; z3 = 91; ![]() = 18; z4 = 36; z5 = 90; КПД одной ступени η = 0,96. Угловая
скорость ведущего звена ω1 = - 500 с-1.
= 18; z4 = 36; z5 = 90; КПД одной ступени η = 0,96. Угловая
скорость ведущего звена ω1 = - 500 с-1.
Решение.
Передаточные
отношения ступеней: i12 = -
z2/z1 = - 83/19 = - 4,37; i23 = z3/![]() =
91/21 = 4,33;
=
91/21 = 4,33; ![]() = 1+ z5/
= 1+ z5/![]() = 1 + 90/18 = 6.
= 1 + 90/18 = 6.
Общее передаточное отношение: i1h = i12 ∙ i23 ∙![]() = - 4,37 ∙ 4,33 ∙ 6 = - 113,53.
= - 4,37 ∙ 4,33 ∙ 6 = - 113,53.
Угловая скорость выходного звена ωh = - 500/(- 113,53) = 4,4 с-1 (звенья 1 и h вращаются в разные стороны).
КПД планетарной передачи – формула (7.30): 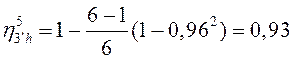 ;
;
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.