Лабораторная работа № 7. Кинематический анализ и синтез зубчатых механизмов., страница 3

Для редуктора Джеймса достаточно условия (7.18).Во внутреннем зацеплении проверяется условие его правильности (отсутствия интерференции) по табл.7.1.

Таблица 7.1

z2	17	18	19	20	21	22	23
z3	∞	>144	>81	>60	>50	>44	>41

Подбор чисел зубьев эпигипоциклического механизма

Решая совместно уравнения (7.10), (7.15) и (7.16), получают расчётные зависимости для подбора чисел зубьев эпигипоциклического механизма (рис. 7.5). Принимают отношения чисел зубьев:

; ,

(7.20)

откуда

; ,

(7.21)

Формула (7.10) для определения передаточного отношения принимает вид:

,

(7.22)

откуда

.

(7.23)

Условие соосности (7.15) с учетом равенств (7.21)...(7.23):

,      , откуда

.

(7.24)

Из условия размещения хотя бы двух сателлитов определяются границы коэффициента x:

< x < .

(7.25)

На основании формул (7.21)...(7.23) составляют пропорцию:

.

(7.26)

Введя в пропорцию (7.26) условие сборки (7.16) и умножая каждый член пропорции на число сателлитов n_c, получают общее расчетное уравнение:

.

(7.27)

На основании пропорции (7.27) можем записать;

,

(7.28)

где  р — постоянный коэффициент.

Призаданном  коэффициент р следует назначать так, чтобы обеспечить целые числа зубьев с наименьшими габаритами редуктора и соблюдением условий кинематики (7.10), соосности (7.15), сборки (7.16), соседства (7.18), (7.19), а также z > z_min  (z_min = 17), обеспечивающего отсутствие подрезания зуба у корня при нарезании колес.

Из формул (7.28) следует, что для получения положительного z₃ передаточные отношения нужно принимать исходя из условия  > 1. Коэффициенты х и у, представляющие собой отношения чисел зубьев, т.е. целых положительных величин, также заведомо положительные числа.

Пример 7.1. Подобрать числа зубьев планетарного редуктора с внешним и внутренним зацеплениями (рис. 7.5) при передаточном отношении = 9 и числе сателлитов n_c =3.

Решение. Определим границы коэффициента х по формуле (7.25):

.

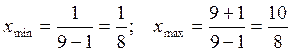Примем х = . Найдем у по формуле (7.24):

.

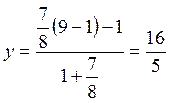Формулы (7.28) запишем в виде:

.

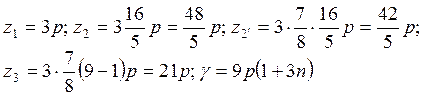Если принять p = 5, то число зубьев z₁ =3∙5 = 15, что меньше допустимого по условию неподрезания. При  p = 10 z₁ =3∙10 = 30, что приведёт к большим габаритам передачи. Все выражения содержат сомножитель 3, поэтому примем дробное 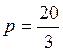, тогда z₁ = 3∙20/3 = 20, z₂ = 48∙20/(3∙5) = 64;  = 42∙20/(3∙5) = 56;   z₃= 21∙20/3 = 140;   = 9∙20(1 +3n)/3 = 60(1 +3n). Число зубьев наименьшего колеса 1 близко к минимально допустимому  (z_min = 17).

         Выполняем проверки:

а) при = 56 и z₃ = 140 интерференции зубьев внутреннего зацепления не будет (см. табл. 7.1);

б) условие кинематики — формула (7.10):

= 9;

в) условие соосности — формула (7.15):

20 + 64 = 140 - 56;  84 = 84;

г) условия соседства — формулы (7.18) и (7.19):

(20 + 64) sin (π/3) - 64 = 8,75 > 2;

(140 - 56) sin (π /3) - 56 = 16,7 > 2;

д) условие сборки — формула (7.26):

γ = 60(1+3n)

равно целому числу при любом п.

Все условия выполнены. Числа зубьев подобраны верно.

Подбор чисел зубьев редуктора Джеймса

Числа зубьев для редуктора Джеймса (рис. 7.4) определяют из следующей пропорции [2]:

.

(7.29)

Из формулы (7.29) следует, что  > +2 (обычно  = 3...8).

    Пример 7.2. Подобрать числа зубьев редуктора Джеймса (рис. 7.4) при передаточном отношении = 7 и числе сателлитов n_c =3.

         Решение.