Лабораторная работа № 7. Кинематический анализ и синтез зубчатых механизмов., страница 2

Передаточное отношение редуктора Джеймса, выраженное через числа зубьев:

В редукторе со сдвоенными сателлитами (эпигипоциклический механизм, рис. 7.5) передаточное отношение

.

(7.10)

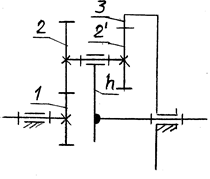
Рис. 7. 5. Эпигипоциклический механизм

        Из формул (7.9) и (7.10) следует, что в редукторе Джеймса и эпигипоциклическом механизме, имеющих наибольшее распространение в машиностроении, солнечное колесо и водило всегда вращаются в одном направлении, так как знак передаточного отношения всегда «плюс».

         В редукторе Давида, имеющем внешние (рис. 7.6) либо внутренние  зацепления, передаточное отношение от водила h к колесу 1 рассчитывают по формуле:

,                                           (7.11) а знак передаточного отношения определяется соотношением между числами зубьев колёс.

 

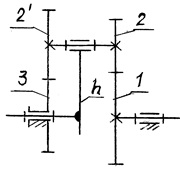
Рис. 7.6. Редуктор Давида с внешними зацеплениями

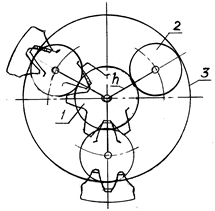
В механизмах класса 3k (рис. 7.7) основными звеньями являются три центральных колеса — 1, 3 и 4. Водило h не является основным звеном и представляет собой конструктивный элемент для поддержания осей сателлитов. Передаточное отношение механизма может быть рассчитано после его разделения на две части: от центрального колеса 1 к водилу h и от водила к другому центральному колесу 4 при остановленном корончатом колесе 3:

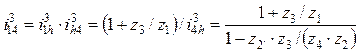             .                                 (7.12)

Рис. 7.7. Механизм класса 3k

В машиностроении и приборостроении часто встречаются редукторы, составленные из обычных и планетарных зубчатых передач. Общее передаточное отношение редуктора определяют по формуле (7.5), в которой одним из сомножителей будет передаточное отношение планетарного механизма.

Планетарные механизмы проектируют с несколькими сателлитами (как правило, 3 или 4), они входят в зацепление с одними и теми же центральными колесами. Это делается для уравновешивания сил инерции и разгрузки зубчатых колес механизма. При определении числа степеней свободы зубчатого механизма все добавочные сателлиты (сверх одного) являются пассивными связями и в структурном анализе не учитываются.

Условия синтеза планетарного механизма

Числа зубьев механизма рассчитывают с учетом условий кинематики — формулы (7.9)...(7.12), соосности, сборки, соседства и правильности внутреннего зацепления (отсутствия в нём интерференции).          

Условие соосности предполагает равенство межосевых расстояний между сателлитом и обоими центральными колесами:

.

(7.13)

В редукторе Джеймса (рис. 7.4) это условие записывают так:

или .

(7.14)

Для эпигипоциклического механизма (рис. 7.5):

.

(7.15)

Необходимость выполнения условия сборки вызывается наличием в планетарном механизме нескольких сателлитов. Если один из сателлитов можно без труда ввести между центральными колесами, то другие могут быть введены в зацепление только при выполнении условия сборки, иначе произойдет интерференция зубьев сателлитов с центральными колёсами, т.е. зуб одного из сателлитов попадет на зуб, а не во впадину центрального колеса (рис. 7.8) и сборка редуктора окажется невозможной. Условие сборки с симметрией зон зацепления записывают следующим образом:

,

(7.16)

где п_с — число сателлитов; п — целое число поворотов водила (n = 0; 1; 2 и т.д.); γ — любое целое число.

Рис. 7.8. Иллюстрация невыполнения условия сборки

Частное решение условия (7.15) для редуктора Джеймса:

,

(7.17)

Условие соседства определяет отсутствие касания соседних сателлитов вершинами зубьев (рис. 7.9), то есть интерференции между соседними сателлитами. Для схемы, приведенной на рис. 7.5, это условие имеет вид:

> 2;	(7.18)
> 2,	(7.19) Рис. 7.9. Интерференция между соседними сателлитами