Случайные функции и случайные процессы, страница 7

3. Ординарность . Для выяснения смысла этого понятия важен пример 2. Ординарность предполагает, что за время  может наступить не более одного события, т.е. реализация СП изменяется скачком на единицу.

Таким образом, реализации  пуассоновского СП представляют собой неубывающую ступенчатую функцию, моменты скачков определяются моментами появления некоторого  события. Значением процесса является число событий, появившихся за время .

Нетрудно показать также, что пуассоновский СП является дискретной марковской цепью. Пусть в моменты  времени    значения процесса были . =

=.

.

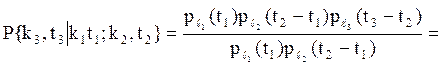
        2.7. Винеровский процесс

Винеровским процессом, выходящим из нуля, называется  СП W(t),, обладающий следующими свойствами:

1. Все реализации  процесса W(t) непрерывны и ;

2.Для любого p=1,2,... и любых значений параметров   его приращения , ,...,  независимы;

3. Случайная величина   имеет нормальное распределение с параметрами , где  - коэффициент диффузии винеровского процесса или его интенсивность.

Таким образом, плотность распределения с.величины , , равна , .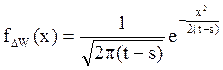

В определении винеровского процесса можно условие  заменить на условие  и тогда получим определение винеровского процесса, выходящего из точки x. Можно рассматривать винеровский процесс, выходящий из случайной точки.

Случайный процесс 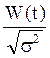 называется стандартным винеровским процессом, его интенсивность равна единице.

Получим конечномерные распределения винеровского процесса. Полагаем                         =1. Зафиксируем N произвольных точек . Случайный вектор  получается из вектора приращений невырожденным линейным преобразованием, матрица которого А, очевидно, имеет вид

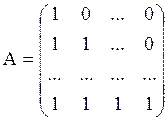,  . Обратная матрица  имеет вид 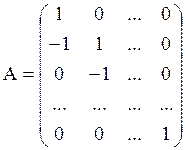 и тогда   и  .

Отсюда, следуя общей теории построения законов распределения функций с. величин, зная плотность распределения с. величины 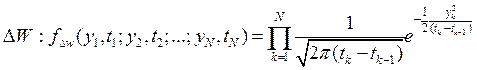, получим плотность распределения с. величины W :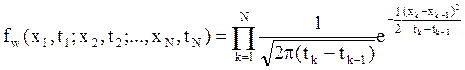, а это плотность многомерного нормального распределения.

Из полученного результата следует , что винеровский процесс является процессом со стационарными приращениями.

Так как винеровский процесс является процессом с независимыми приращениями, то согласно формуле  (5)   .

Если   W(t), , с. вектор, то все компоненты его независимы и представляют собой одномерные винеровские процессы. Для такого процесса .

Винеровский процесс называют еще процессом броуновского движения; он имел большое значение при разработке теории СП. Многие распределения, используемые в теории управления, можно моделировать процессами, порождаемыми винеровскими процессами. 

Отметим,  что распределение винеровского процесса можно получить с использованием характеристических функций. Так как  винеровский процесс – это СПНП, поэтому его характеристическая функция  представима в виде

.

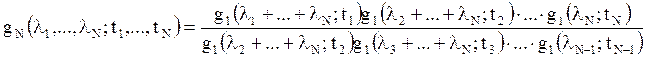Одномерная характеристическая функция винеровского процесса , 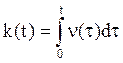. Подставив это выражение в формулу для  после громоздких, но несложных вычислений находим

.

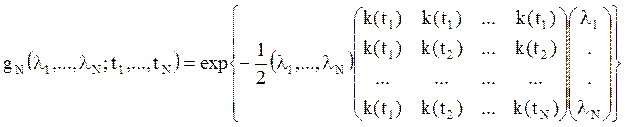Эта формула более информативна. Из нее, в частности, следует, что ,  , что вполне отвечает условию, что винеровский процесс является СПНРП.

Траектория винеровского процесса обладает весьма неожиданными свойствами. В дальнейших главах покажем, что сумма квадратов приращений винеровского процесса, соответствующих разбиению отрезка  точками , при стремлении мелкости разбиения  к нулю, сходится в смысле средней квадратической сходимости к .Если рассмотреть аналогичную сумму квадратов приращений для процесса, изменяющегося скачками, то она будет конечной на любом отрезке , если число скачков на отрезке конечно, и совпадает с суммой квадратов скачков, таким образом, не зависит непрерывно от a  и b.

Сравнение этих результатов приводит к вопросу о том, существует ли у траектории винеровского процесса скачки.

А.Н. Колмогоров показал, что для любого винеровского процесса можно построить новый, эквивалентный ему процесс с непрерывными траекториями. В силу того, что конечномерные распределения эквивалентных процессов совпадают, новый процесс с независимыми приращениями также будет винеровским. Этими соображениями и продиктовано условие 1) в определении винеровского процесса.