Случайные функции и случайные процессы, страница 2

         1.3. Моменты случайной функции

Казалось бы естественным рассматривать СП  X(t), ,  как всю совокупность случайных  величин Х. Но в общем случае это множество с. величин может быть  несчетным и невозможно  построить совместный закон распределения  всех   его сечений.  При решении практических задач по многим причинам используются одно- и двумерные законы распределения и связанные с ними моменты первого и второго порядков, существование которых предполагается.Отметим, что моментом k-го порядка СП X(t) называется k-ый момент его сечений .

       Определение 1. Математическим ожиданием (м.о.) СП  X(t),, называют неслучайную функцию  переменной  , которая при всех  равна математическому ожиданию с.величин – сечений  СП X(t).

Итак, 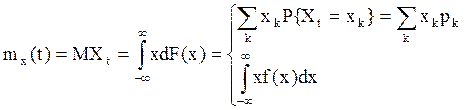, при этом  ,  .

Функцию  ,  ,   интерпретируют  как усредненную реализациюпроцесса  X(t).

        Определение 2.  Ковариационной функцией (функцией ковариаций) СП  X(t), , называютнеслучайную матричную функцию  размерности  скалярных переменных , значения которой при любых фиксированных   равно ковариации двух случайных векторов  и :

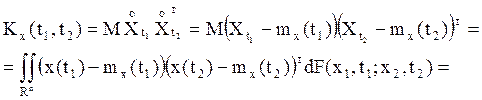
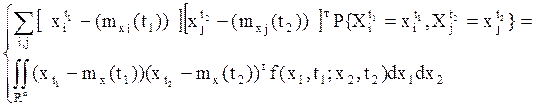
при этом  и

 – двумерная плотность распределения СП  X(t), .

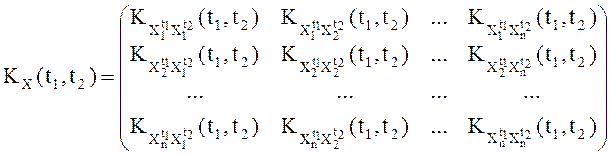
При  фиксированных   элементами матрицы   являются ковариации с.величин  и ,  .  

Если , то ковариационная функция называется ковариационной матрицей, ее элементы при фиксированном t определяют ковариации случайного вектора X_t. Обозначают K_x(t, t) через D_x( t ) и называют дисперсией СП X( t ).

Выше мы записали определение   через двумерную плотность СП X(t). При  двумерное распределение оказывается сосредоточенным на прямой , то есть является вырожденным. В этом случае двумерная плотность распределения выражается через ее одномерную плотность формулой:

.

Тогда формула для дисперсии D_x(t) СП  X(t) примет вид:

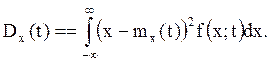
          Пример 1.   Найти математическое ожидание и ковариационную функцию действительной  ступенчатого СП  X(t), который скачком  меняет свое значение в случайные моменты времени, образующие пуассоновский поток интенсивности , а в промежутках между этими моментами  сохраняет неизменные значения, представляющие собой независимые случайные величины с нулевыми м.о. и постоянными дисперсиями .

Очевидно, что , и поэтому  (n=1). Введем вспомогательную с.величину

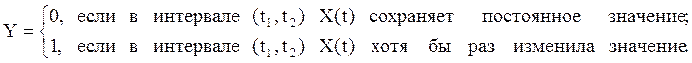
Из теории вероятностей известно, что число точек изменения значения СП X(t), попадающих в интервал (t_1, t₂), распределено по закону Пуассона с параметром , поэтому   ,  . Следовательно, плотность распределения с.величины Y определяется формулой:   .

Далее для вычисления  применим  формулу полного математического ожидания:

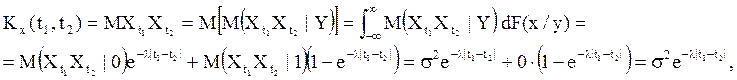
так как ,  .

Пример 2. Случайная функция N(t) удовлетворяет следующим условиям:

1.  N(t) определена ;

2. ;

3. Для любых  с.величины ,  независимы;

4. В случайный момент времени происходит приращение значения функции  на единицу, причем для любого момента времени t≥0    , , и

- постоянное для данного процесса число. Найти одномерное распределение СП N(t).

Введем обозначения. Разность   обозначим через . Это случайное приращение процесса за время ∆t. Положим  , n=0, 1, 2…  Задача состоит в отыскании       для n=0, 1, 2 … и всех . Событие    означает, что «число единичных приращений за время t равно n». Выразим  событие  следующим образом: .

По условию 3 задачи, полагая, ,   получаем, что случайные величины         независимы. Поэтому пары событий в правой части записанного выше равенства так же независимы. По условию 4

, , . Тогда

.

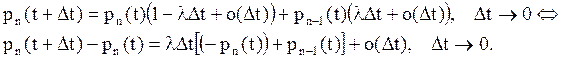Деля обе части полученного равенства на ∆t и переходя к пределу при ∆t→0, получим дифференциальное уравнение для искомых вероятностей:

 n=0,1,2,…с начальными условиями , n=1,2,…

Дифференциальное уравнение решаем рекуррентно, считая, что на n-м шаге значение  уже известно.

Пусть  n=0.  Дифференциальное уравнение принимает вид   при ограничении . Решая это уравнение, перепишем его в виде:

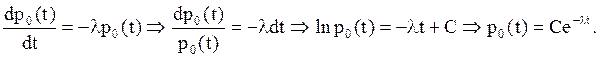
Поскольку  окончательно имеем .

Итак, мы получили вероятность того, что в интервале (0, t) не произойдет ни одного события.