Случайные функции и случайные процессы, страница 4

_.  В последнем неравенстве использовано свойство 2 ковариационных матриц. Далее  =

 =

.  Следовательно,     .

5. Пусть X(t)- некоторый  СП и - неслучайная функция переменной t , А(t)-матричная неслучайная функция и Y(t) = А(t) X(t)+ . Тогда  . ( Проверить самостоятельно).

  I.          II. Некоторые классы случайных процессов

Опишем некоторые классические типы СП, характеризующиеся различными видами зависимости между .

       2.1. Стационарные процессы

СП Х(t) ,, называется стационарным в узком смысле, если совместное распределение с. величин  и  одинаковы при всех  h и всех,. Это условие означает, что процесс  находится в вероятностном равновесии и момент начала наблюдения  за ним не имеет значения . В частности , распределение с. величин  одно и то же при всех t. Формально условие стационарности СП в узком смысле можно записать так:     или, что то же самое,

.

При n=1 это условие имеет вид: . Полагая, получим

 - одномерное распределение  стационарного СП не зависит от времени. Одномерное же распределение СП определяет  математическое ожидание СП,  следовательно,

                                                  (2)

При n=2 из условия стационарности (1) следует:.

Полагаем h=-t_1, имеем  . Следовательно, двумерное распределение стационарного СП зависит только от разности . Но тогда и ковариационная  функция СП есть функция одного параметра τ:

.                                           (3)

Условия (2),(3) зачастую проверить легче, чем  условие (1).

СП Х(t) ,, называют стационарным в широком смысле, если он обладает конечными вторыми моментами (а значит и первыми), и его математическое ожидание не зависит от времени, а ковариационная  функция   зависит только от разности  .

Иначе, СП  Х(t) ,, является стационарным в широком смысле, если для него выполнены условия (2),(3).

Из стационарности в узком смысле следует стационарность в широком смысле (что и было показано выше). Обратное утверждение справедливо только для гауссовских (нормальных)  процессов ( их определение  приведено ниже ).

Далее везде под словами “стационарный процесс” будем понимать стационарный СП в узком смысле.

Простым примером стационарного процесса является любой процесс, состоящий из независимых одинаково распределенных случайных величин.

        Пример 3. Пусть СП X(t) имеет вид ,, и  - положительные с.величины, имеющие плотность распределения , с. величина  не зависит от  и и распределена по равномерному закону на отрезке . Докажем, что СП X(t) является стационарным.

Начнем с его одномерного распределения. Фиксируем . Сечением процесса будет с.величина . Плотность распределения сечения  можно найти в два этапа. Сначала найдем совместную плотность распределения с.величин  и , затем искомую плотность распределения с.величины  . Для этого запишем соотношение для реализаций случайных величин:

u=

v= -   ввели новые переменные,         

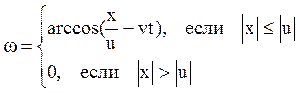
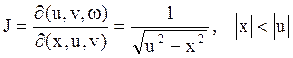.Согласно теории построения законов распределенияфункций случайных величин, находим:

 

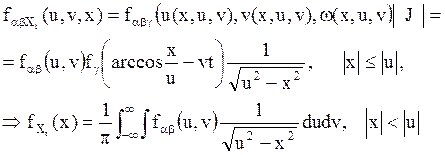
Полученное выражение показывает, что одномерная плотность распределения  не зависит от t.

Для   фиксируем точки   , определяем  закон распределения

N-мерного с. вектора с компонентами , ,  остается показать, что

. Принципиальная схема рассуждений аналогична использованной в одномерном случае.

        2.2. Случайные процессы с некоррелированными приращениями

СП  X(t), , называется процессом с некоррелированным приращениями (СПНРП),если для любых не пересекающихся интервалов , , , соответствующие приращения ,   процесса X(t) не коррелированны.

Таким образом, СП X(t) является СПНРП, если . Из этого определения следует, что приращения процесса с некоррелированными приращениями  на любых конечных интервалах имеют конечные моменты второго порядка. При этом сам процесс может и не иметь конечных математического ожидания и момента второго порядка.

Однако, если в некоторый момент  значение СПНРП X(t) почти наверное равно нулю,  , то X(t) имеет конечные моменты первого и второго порядков, так как его значение в любой момент t совпадает с его приращением на интервале  при   и его приращением на интервале , взятом с противоположным знаком при .