Пусть теперь n=1. При этом
значении n получаем линейное неоднородное уравнение с
начальными условиями: ![]()
![]() .
.
Общее решение соответствующего однородного
уравнения есть ![]() . Частное решение неоднородного
уравнения, найденного методом вариации постоянной, имеет вид:
. Частное решение неоднородного
уравнения, найденного методом вариации постоянной, имеет вид: ![]() .
.
Тогда общее решение уравнения получаем в виде: ![]() . Начальные условия
. Начальные условия ![]() дают
для С значение 0, С=0.
дают
для С значение 0, С=0.
Окончательно имеем: ![]() .Тем самым, вероятность того, что в
интервале времени (0, t) произойдет
ровно одно событие, найдена.
.Тем самым, вероятность того, что в
интервале времени (0, t) произойдет
ровно одно событие, найдена.
Рассуждая
аналогично, для ![]() , можно получить следующие
результаты:
, можно получить следующие
результаты: 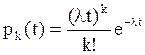 ,
, ![]()
![]() .
.
Случайный процесс N(t), t≥0, называется пуассоновским.
Параметр ![]() трактуется как среднее число единичных
приращений в единицу времени.
трактуется как среднее число единичных
приращений в единицу времени.
Ковариационная функция СП Х(t)
является вторым смешанным центральным моментом с. величин ![]() и
и ![]() . Иногда
вместо нее рассматривают второй смешанный начальный момент
. Иногда
вместо нее рассматривают второй смешанный начальный момент ![]() . Эту функцию называют корреляционной
функцией СП Х(t). Из теории вероятностей известно
соотношение между этими функциями:
. Эту функцию называют корреляционной
функцией СП Х(t). Из теории вероятностей известно
соотношение между этими функциями:
![]() =
=![]() -
-![]() или
или ![]() =
=![]() +
+![]() (2)
(2)
Определение 3. Взаимной ковариационной
функцией KXY(t1,
t2) случайных функций X(t) и Y(t),
определенных на одном и том же вероятностном пространстве и на одном и том же
множестве Т, называется ковариация их сечений ![]() ,
рассматриваемая как функция аргументов
,
рассматриваемая как функция аргументов ![]() :
: ![]() ,
, ![]() ,
, ![]() .
.
Если для любых ![]()
![]() , то случайные процессы X(t), Y(t)
называются некоррелированными. Если хотя бы для одной пары
, то случайные процессы X(t), Y(t)
называются некоррелированными. Если хотя бы для одной пары ![]()
![]() , то X(t), Y(t)
называются коррелированными случайными функциями.
, то X(t), Y(t)
называются коррелированными случайными функциями.
Аналогичным образом определяется взаимная корреляционная функция процессов
1.4. Белый шум
Большое значение для приложений имеет особый вид случайных функций, у которых ковариационная функция содержит множителем δ-функцию.
Определение
4. СП X(t), ![]() , с нулевым м.о. и ковариационной функцией
, с нулевым м.о. и ковариационной функцией
![]() называется белым шумом. Множитель
называется белым шумом. Множитель ![]() называется интенсивностью белого шума.
называется интенсивностью белого шума.
Очевидно,
что дисперсия Dx(t) белого шума бесконечна ![]() ,
а его значения в двух сколь угодно близких точках не коррелированны.
,
а его значения в двух сколь угодно близких точках не коррелированны.
В чистом виде белый
шум не может существовать физически, для его реализации необходима бесконечная
мощность. Поэтому понятие белого шума является математической абстракцией, удобной для
построения теории. Практически можно говорить о большей или меньшей степени
приближения случайной функции к белому шуму. Это можно сделать только в том
случае, когда наименьший интервал между значениями аргумента, при которых
значения случайной функции практически не коррелированны, называемый интервалом
корреляции, достаточно мал. Если 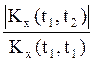 для скалярного СП X(t) можно считать практически равной
0 при
для скалярного СП X(t) можно считать практически равной
0 при ![]() и величина
и величина ![]() достаточно
мала, то СП X(t) можно
считать белым шумом интенсивности
достаточно
мала, то СП X(t) можно
считать белым шумом интенсивности 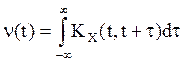 .
.
Ясно, что понятие интервала корреляции не является математически точным. Это чисто практическая мера близости случайных функций к белому шуму. Практически для случайных функций X(t) интервал корреляции определяется формулой:
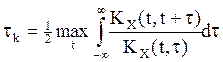 .
.
Векторную случайную функцию X(t) можно считать белым шумом, если все ее компоненты допустимо принять за белый шум.
1.5. Свойства моментов второго порядка
1. ![]() .
.
Действительно, 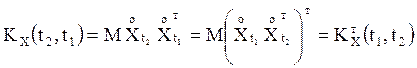 . Для
скалярного процесса X(t)
. Для
скалярного процесса X(t) ![]() .
.
2. Матрица ![]() является неотрицательно определенной
функцией
является неотрицательно определенной
функцией ![]() .
.
По определению таких функциональных матриц это
означает, что ![]() ,
, ![]() , и
векторов
, и
векторов ![]() той же размерности, что и СП X(t),
той же размерности, что и СП X(t), 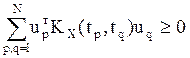 .
.
Действительно
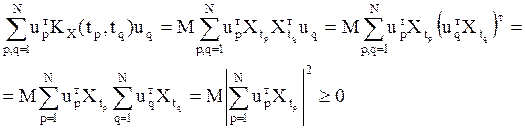
Здесь использовано
свойство: для любых векторов a и b одной размерности n 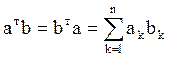 .
.
3.![]() , где
, где ![]() .
.
Нормой матрицы будем считать
евклидову норму. Это свойство называют неравенством Коши- Буняковского. Оно
следует из неравенства Шварца для математического ожидания : ![]() векторных с. величин
векторных с. величин ![]() ,
, ![]() .
.
Пусть ξ и η –
скалярные с. величины. Имеем ![]() λ
λ![]() R 0
R 0![]()
![]() дискриминант квадратного трехчлена
относительно λ неположителен:
дискриминант квадратного трехчлена
относительно λ неположителен: 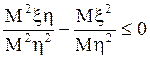
![]() .
Используя его для векторных с. величин, получим
.
Используя его для векторных с. величин, получим 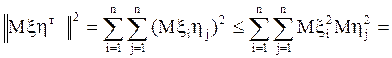
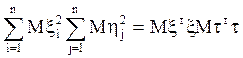 .
.
Если теперь в качестве
ξ взять с. величину ![]() -
-![]() , вместо
η- с. величину
, вместо
η- с. величину ![]() -
-![]() ,
тогда
,
тогда ![]()
![]() ;
;
![]() .
.
4. Если ![]() непрерывна в точках
непрерывна в точках ![]() , то она непрерывна во всех точках квадрата
T
, то она непрерывна во всех точках квадрата
T![]() T.
T.
Оценим разность : ![]()
![]()
![]()
![]() +
+![]()
![]() *
*
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.