Случайные функции и случайные процессы, страница 6

Функции  называют вероятностями перехода из состояния в состояние , обозначают  как .Вероятности перехода удовлетворяют двум основным соотношениям:

1.Условию нормировки -                                         (9)

2.Уравнению Чепмена-Колмогорова –

                              (10)

для любых , соответствующих моментам времени .

  2.5. Нормальные (гауссовские) процессы

СП  X(t), , называется гауссовским (нормально распределенным), если все его конечномерные распределения нормальны.

Напомним некоторые сведения из теории вероятностей. Скалярная с. величина  называется гауссовской (нормально распределенной) с параметрами a и , , , если она имеет плотность распределения  вид: 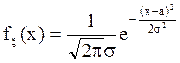.  Параметры a и  имеют простой смысл: , .

Характеристической функцией скалярной с.величина  называется комплекснозначная функция 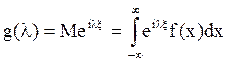 . Для гауссовской с.величина  характеристическая функция имеет вид:  .

Случайный вектор , , ,  называется гауссовским или нормально распределенным, если его плотность задается формулой: 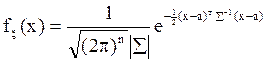,   где ,, ,   .  В невырожденном случае, когда матрица положительно определена, такое определение гауссовского вектора корректно. Если же гауссовское распределение имеет матрицу  такую, что , то его удобно определить через характеристическую функцию:  , где   и - вектор той же размерности, что и вектор . В частном случае, когда двумерный гауссовский  вектор  имеет невырожденное распределение, его плотность записывается в ви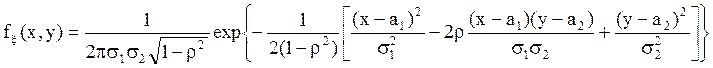де:

,  где , , 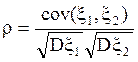то есть матрица  представима виде:.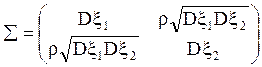

Характеристическая функция вектора  в этом случае имеет вид:

,  .

Известно, что 1) если n-мерный вектор  имеет нормальное распределение, то и компоненты этого вектора так же имеют нормальное распределение; 2) если  - независимые гауссовские с.величины, то вектор  также является гауссовским;   3) всякий подвектор гауссовского вектора является гауссовским.

В заключение рассмотрим структуру вырожденного гауссовского распределения. Пусть . Тогда каждую с.величину , , с вероятностью 1 можно представить в виде линейной комбинации r независимых с.величин . При условии, что , этот факт означает, что все распределение вектора  сосредоточено в r-мерном подпространстве  пространства . Если снять условие , то все распределение      с. вектора  сосредоточено на некоторой гиперплоскости пространства   вида .  

Приведем без доказательства теорему, отвечающую на вопрос: для заданного вектора a размерности n и симметричной неотрицательно определенной матрицы R порядка  существует ли гауссовский СП, определенный на данном параметрическом множестве T, и такой, что его  характеристики совпадают с заданными вектором a и матрицей R.

        Теорема 1. Пусть даны T – произвольное множество, a(t) – произвольная функция с действительными значениями, R – симметричная неотрицательно определенная матрица . Тогда существует вероятностное пространство  и семейство случайных величин  на нем, такие что ,  .

        2.6. Пуассоновский процесс

Пуассоновским процессом с параметром называется СП X(t), , обладающий следующими свойствами:

1.  ;

2. Для любого  p=1,2,...  и любых значений параметров   его приращения , k=1,2,..., p, независимы;

3. Случайная величина , , имеет пуассоновское распределение с параметром , то есть .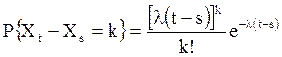

Пуассоновский процесс возникает при моделировании потока редких событий. Он играет важную роль в различных приложениях теории СП, в частности, в теории массового обслуживания.

Пример 2 и определение пуассоновского процесса позволяют перечислить некоторые важные свойства этого процесса.

1. Отсутствие последействия. Число наступлений событий  в некотором интервале не зависит от числа наступлений событий в других , непересекающихся с ним интервалах ,           – условие 2 в определении;

2. Стационарность. Число событий, наступивших на интервале , не зависит от положения этого интервала на числовой прямой, от значения процесса в точке s, а определяется полностью длиной интервала  (t-s) – условие 3  в определении;