Далее будем рассматривать только такие СПНРП,
тем более, что любой СП Y(t) сводится к такому процессу. Достаточно рассмотреть
процесс ![]() ,
, ![]() - фиксированная точка из T,
тогда
- фиксированная точка из T,
тогда ![]() .
.
Из определения также следует, что значение ![]() процесса X(t) в
любой момент t не коррелированно с его будущими приращениями на
интервалах, следующих за моментом
процесса X(t) в
любой момент t не коррелированно с его будущими приращениями на
интервалах, следующих за моментом ![]() , и с его прошлыми
приращениями на интервалах, предшествующих моменту
, и с его прошлыми
приращениями на интервалах, предшествующих моменту ![]() :
:
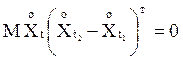 при
при ![]()
![]() и
и ![]() ,
, ![]() .
.
Этот факт становится очевидным, если учесть,
что ![]() есть приращение процесса X(t) на
интервале
есть приращение процесса X(t) на
интервале ![]() , не пересекающимся с
, не пересекающимся с ![]() при
при ![]() , и
взятое с противоположным знаком приращение процесса X(t) на
интервале
, и
взятое с противоположным знаком приращение процесса X(t) на
интервале ![]() , не пересекающимся с
, не пересекающимся с ![]() при
при ![]() .
.
СПНРП описывают с
помощью функции ![]() , равной
, равной
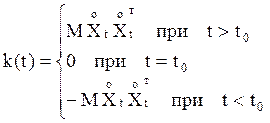 (4)
(4)
Справедливо утверждение, что ковариационная
функция процесса X(t) и ковариационная матрица приращения ![]() процесса X(t) на
любом интервале определяется следующими формулами:
процесса X(t) на
любом интервале определяется следующими формулами:
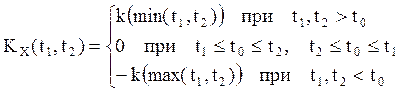 ;
(5)
;
(5)
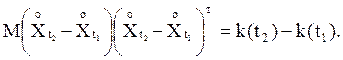 (6)
(6)
Из определения
функции k(t) ясно, что при ![]() она представляет собой ковариационную
матрицу значения процесса X(t)
в момент t, при
она представляет собой ковариационную
матрицу значения процесса X(t)
в момент t, при ![]() -
взятую с противоположным знаком ковариационную матрицу значения процесса X(t) в момент t.
Приращение функции k(t) на
любом интервале служит ковариационной матрицей приращения процесса X(t) на интервале. Из этих фактов
следует, что k(t) –
неубывающая, неотрицательная при
-
взятую с противоположным знаком ковариационную матрицу значения процесса X(t) в момент t.
Приращение функции k(t) на
любом интервале служит ковариационной матрицей приращения процесса X(t) на интервале. Из этих фактов
следует, что k(t) –
неубывающая, неотрицательная при ![]() , неположительная при
, неположительная при ![]() , равная нулю при
, равная нулю при ![]() функция.
функция.
Верно и обратное
утверждение: если ковариационная функция СП X(t) определяется формулой (5), и k(t) при этом функция с перечисленными выше свойствами, то X(t)-СПНРП, значение которого в
момент ![]() почти наверное равно 0.
почти наверное равно 0.
Таким образом, возможность представления ковариационной функции процесса через
функцию k(t) с указанными выше свойствами является необходимым и
достаточным условием того, что X(t)-СПНРП и его значение при ![]() равно
нулю почти наверное.
равно
нулю почти наверное.
Полагая в дальнейшем функцию k(t) непрерывной и дифференцируемой, выражение для ![]() может быть переписано в виде при
может быть переписано в виде при ![]()
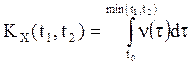 ,
(7), где
,
(7), где ![]() -
неотрицательная функция, называемая интенсивностью СПНРП.
-
неотрицательная функция, называемая интенсивностью СПНРП.
2.3. Процессы с независимыми приращениями
СП X(t), ![]() , называется процессом с независимыми
приращениями(СПНП), если для любых
, называется процессом с независимыми
приращениями(СПНП), если для любых ![]() и
и ![]() ,
, ![]() , таких,
что
, таких,
что ![]() , с.величины
, с.величины
![]() являются
независимыми. По определению независимых с. величин
являются
независимыми. По определению независимых с. величин ![]()
![]()
![]()
![]() . Если
. Если ![]() - наименьший среди всех индексов, то
предполагается также, что
- наименьший среди всех индексов, то
предполагается также, что ![]() независимы. Если Т={0,1,2,…},
то СПНП сводится к последовательности независимых с. величин
независимы. Если Т={0,1,2,…},
то СПНП сводится к последовательности независимых с. величин ![]() Если знать распределения с. величин
Если знать распределения с. величин ![]() , к=1,2,… , то можно определить совместное
распределение любого конечного числа с. величин
, к=1,2,… , то можно определить совместное
распределение любого конечного числа с. величин ![]() , так
как
, так
как ![]() .
.
Если процесс с независимыми приращениями имеет
конечный момент второго порядка, то он является процессом с некоррелированными
приращениями. Следовательно, в этом случае ковариационная функция ![]() СПНП X(t)
определяется формулой:
СПНП X(t)
определяется формулой:
![]() , где k(t) – неубывающая неотрицательная функция, представляющая собой ковариационную матрицу (
дисперсию в случае скалярного процесса X(t))
значения процесса X(t) в данный момент t. Если k(t) –
непрерывная и дифференцируемая функция, то
, где k(t) – неубывающая неотрицательная функция, представляющая собой ковариационную матрицу (
дисперсию в случае скалярного процесса X(t))
значения процесса X(t) в данный момент t. Если k(t) –
непрерывная и дифференцируемая функция, то 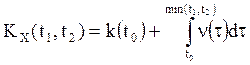 и
и ![]() - интенсивность СПНП.
- интенсивность СПНП.
2.4. Марковские процессы
СП X(t), ![]() , называется марковским СП (МП) если для
всех n>1 и любых
, называется марковским СП (МП) если для
всех n>1 и любых ![]() его
условное распределение в момент времени
его
условное распределение в момент времени ![]() не
зависит от значений процесса в моменты
не
зависит от значений процесса в моменты ![]() , а
определяется значением процесса в момент времени
, а
определяется значением процесса в момент времени ![]() , то
есть
, то
есть ![]() (8)
(8)
Если пространство состояний МП Х счетно
и множество Т имеет вид Т={![]() }
,то МП называется марковской цепью . Еслимножество Х счетно, а
множество Т- непрерывное множество, то МП называют МП с дискретными
состояниями или дискретным МП. Если Х и Т непрерывные множества, то
МП называют непрерывным марковским процессом.
}
,то МП называется марковской цепью . Еслимножество Х счетно, а
множество Т- непрерывное множество, то МП называют МП с дискретными
состояниями или дискретным МП. Если Х и Т непрерывные множества, то
МП называют непрерывным марковским процессом.
Рассмотрим
многомерную плотность распределения МП: ![]()
![]()
![]() . Следовательно,
непрерывный МП
. Следовательно,
непрерывный МП
однозначно определяется своим двумерным распределением
(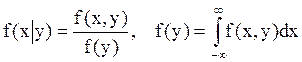 ).
).
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.