![]()
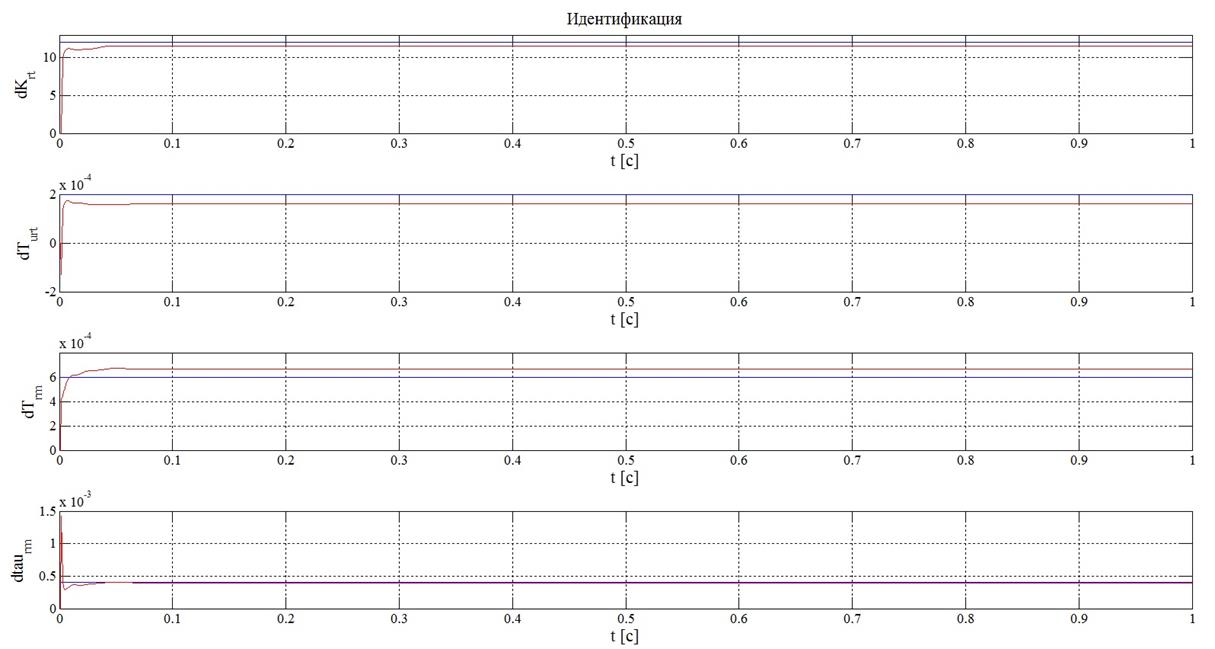
![]() Рисунок
19 – Результаты идентификации при задающем воздействии, равном константе и
Рисунок
19 – Результаты идентификации при задающем воздействии, равном константе и ![]()
![]()
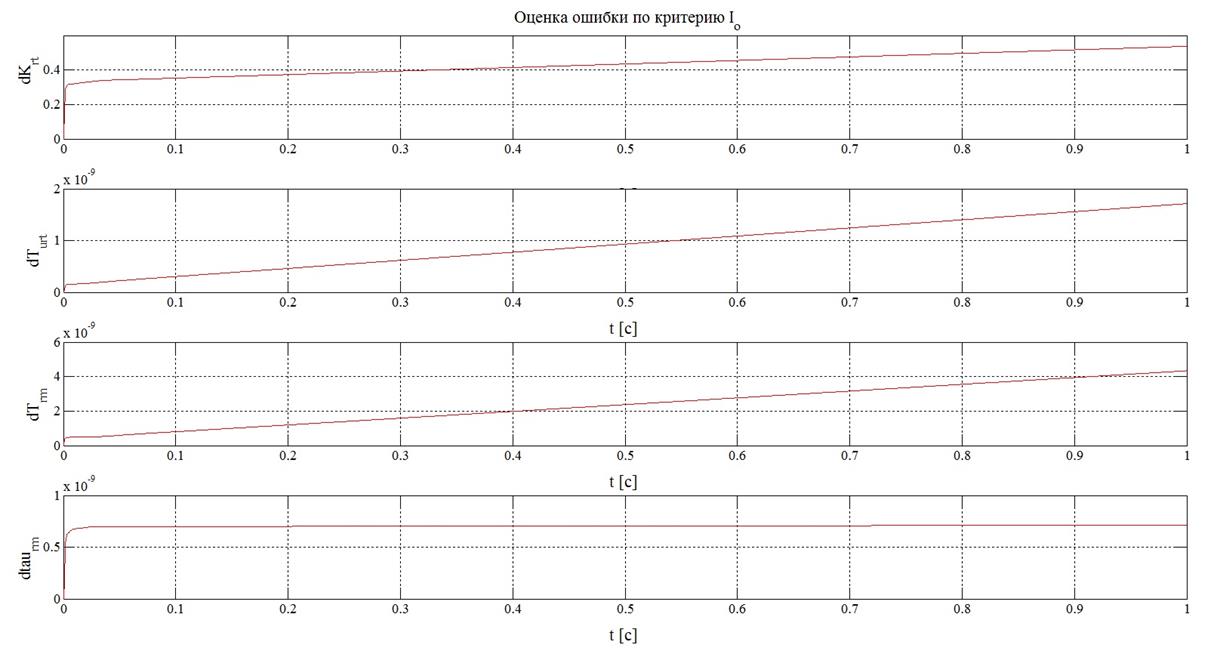
Рисунок 20 – Результаты
оценки с помощью критериев (14) при задающем
воздействии, равном константе и ![]()
![]()
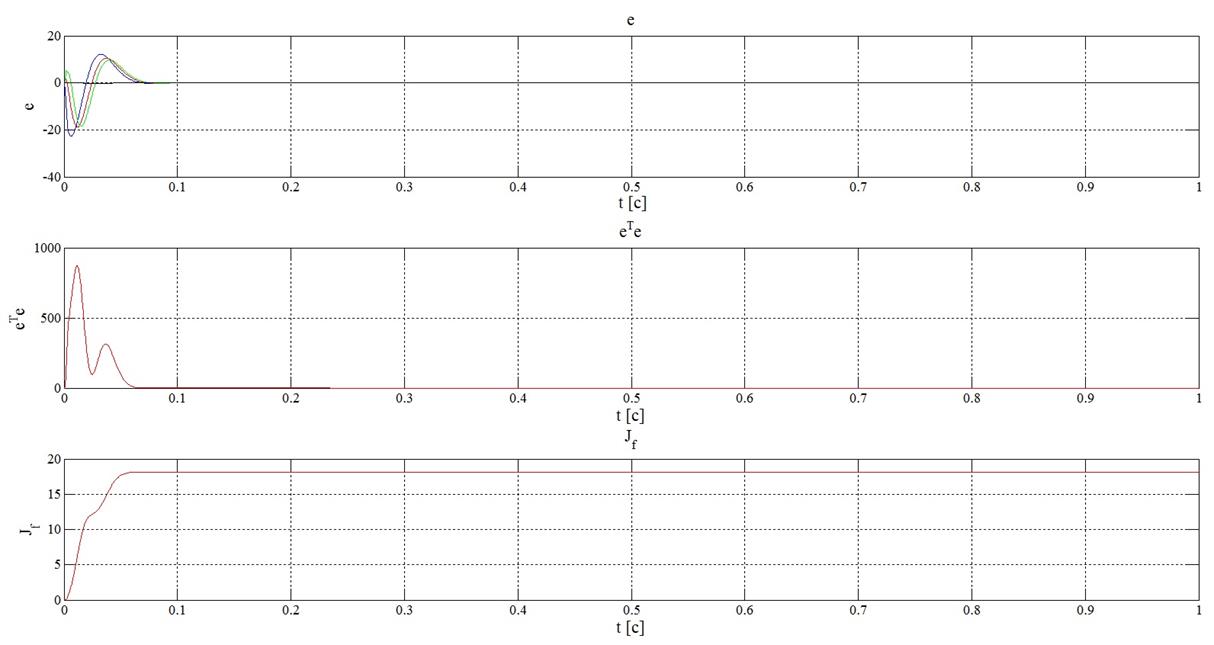
Рисунок 21 – Результаты
оценки с помощью критериев (15), (16) и (17) при задающем
воздействии, равном константе и ![]()
![]()
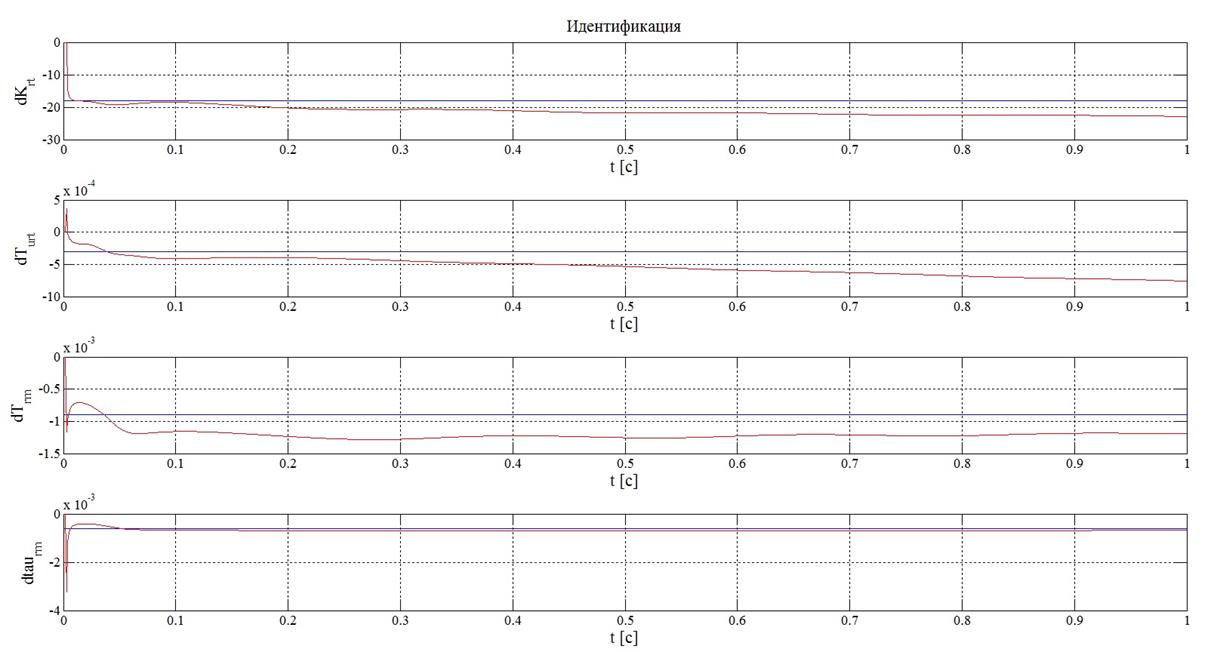
![]() Рисунок
22 – Результаты идентификации при синусоидальном задающем воздействии и
Рисунок
22 – Результаты идентификации при синусоидальном задающем воздействии и ![]()
![]() \
\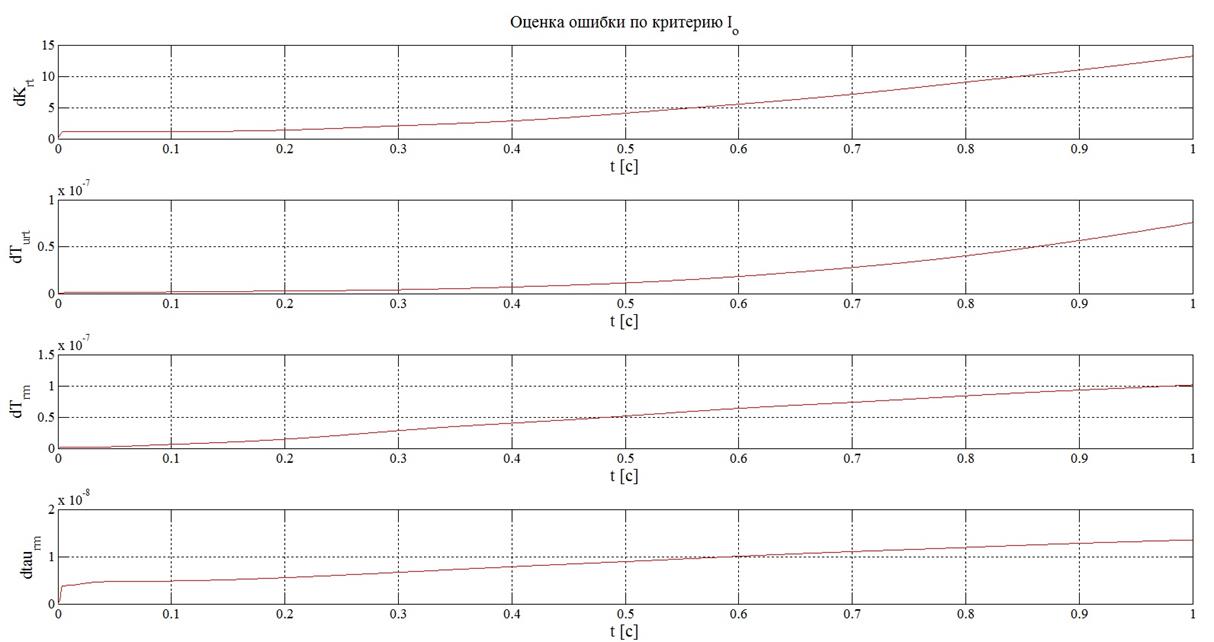
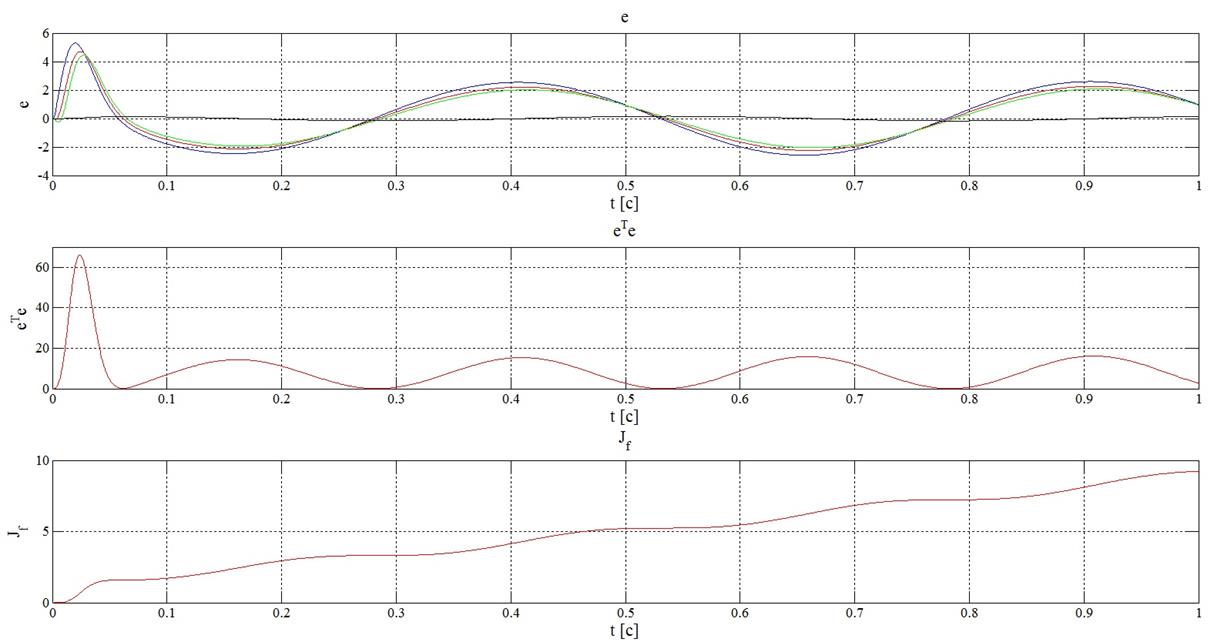
Рисунок 23 – Результаты
оценки с помощью критериев (14) при синусоидальном задающем воздействии и ![]()
![]()
Рисунок 24 – Результаты оценки с помощью критериев (15), (16) и (17) при синусоидальном задающем воздействии и
![]()
![]()
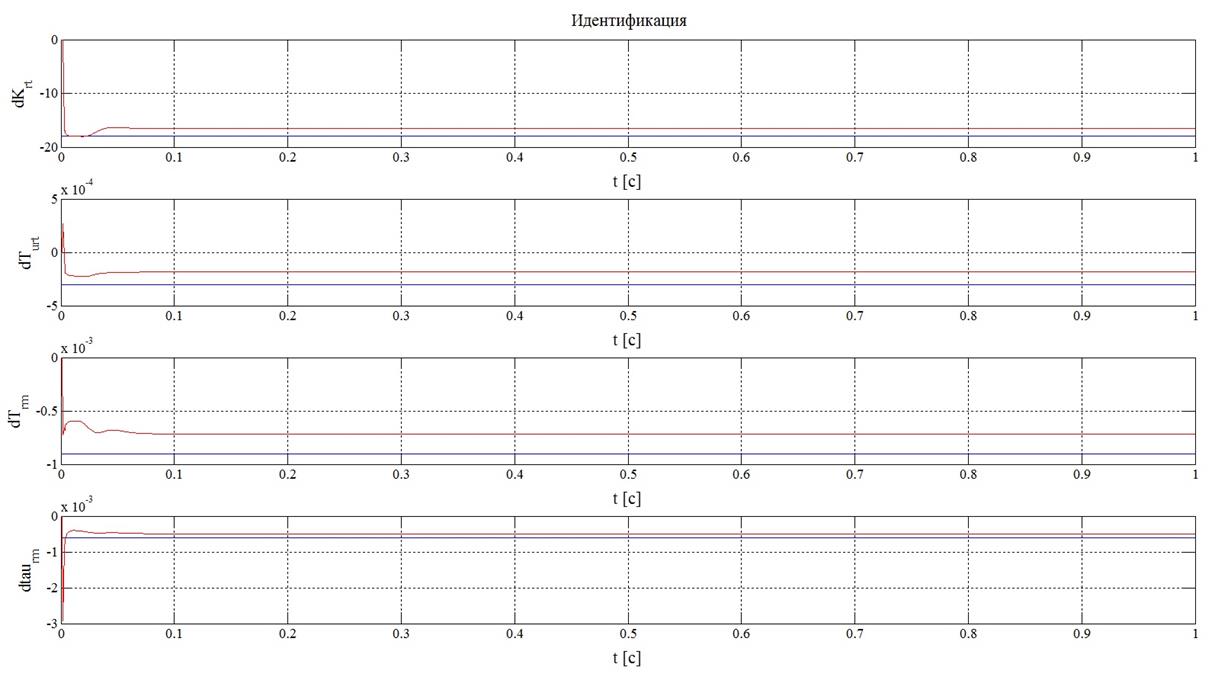
![]() Рисунок
25 – Результаты идентификации при задающем воздействии, равном константе и
Рисунок
25 – Результаты идентификации при задающем воздействии, равном константе и ![]()
![]()
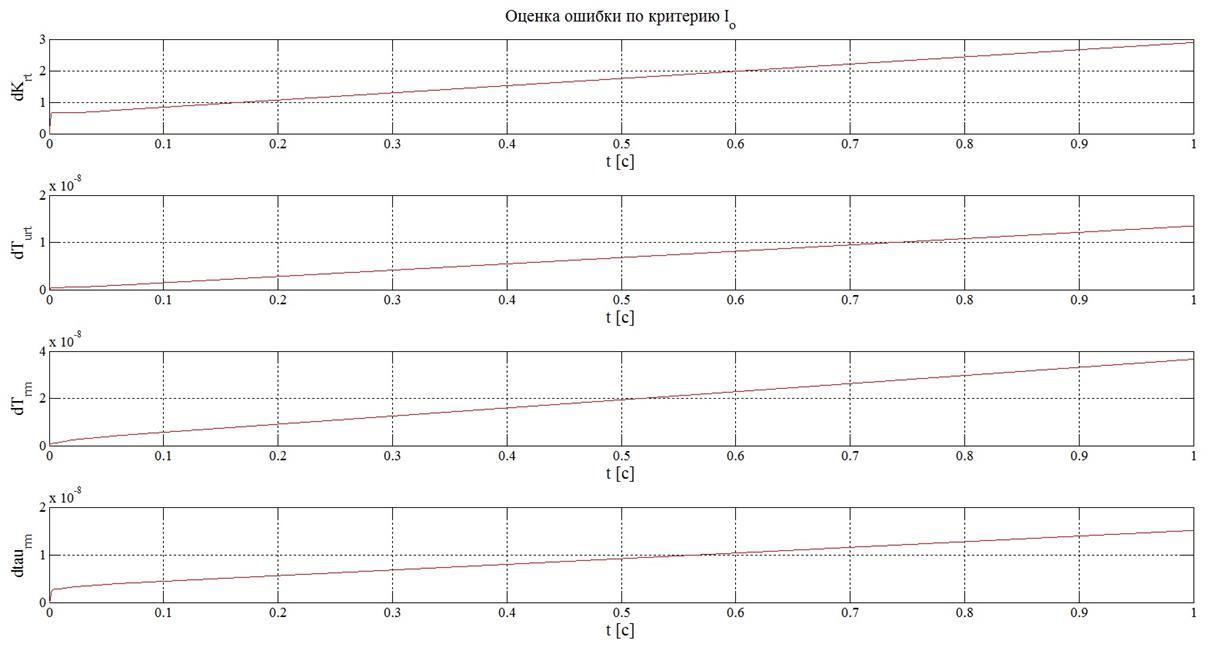
Рисунок 26 – Результаты
оценки с помощью критериев (14) при задающем воздействии, равном константе и ![]()
![]()
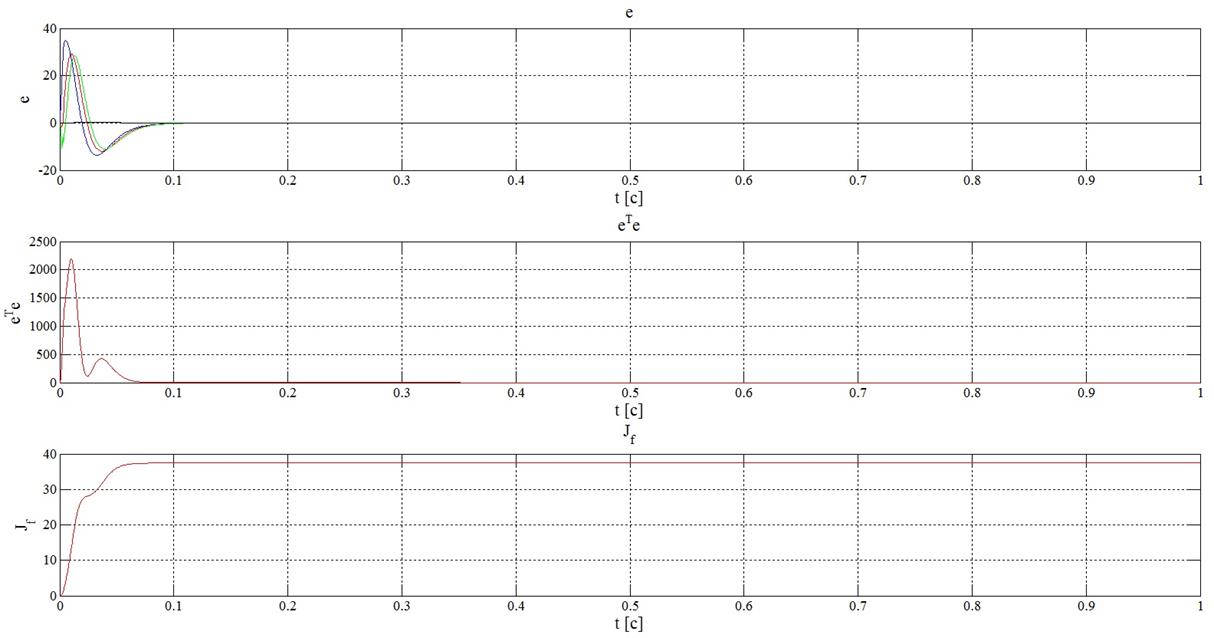
![]() Рисунок 27 – Результаты оценки с помощью критериев (15), (16) и (17)
при задающем воздействии, равном константе и
Рисунок 27 – Результаты оценки с помощью критериев (15), (16) и (17)
при задающем воздействии, равном константе и ![]()
ЗАКЛЮЧЕНИЕ
Существует множество вариантов реализации алгоритма идентификации, каждый из которых по-своему отличается в лучшую сторону. Отличия могут заключаться как в быстродействии системы при реализации на ПЭВМ, так и в точности идентифицируемых параметров.
В выполненном проекте рассматривался базовый метод наименьших
квадратов. За основу была взята модель рулевого привода летательного аппарата,
параметры которого и были идентифицированы. Из результатов видно, что
использование функций чувствительности в задачах идентификации параметров ![]() приемлемо, но модель
идентификации требует существенных доработок для достижения наилучшей точности.
приемлемо, но модель
идентификации требует существенных доработок для достижения наилучшей точности.
В ходе работы также была построена универсальная программа для
идентификации параметров с удовлетворяющей точностью, на входы которой
поступают матрица чувствительности ![]() и изменение выходного
сигнала
и изменение выходного
сигнала ![]() . Универсальность
программы заключается в том, что матрица
. Универсальность
программы заключается в том, что матрица ![]() может иметь любую
размерность.
может иметь любую
размерность.
1. Розенвассер Е. Н., Юсупов Р. М., Вклад ленинградских ученых в развитие теории чувствительности систем управления: Тр. СПИИРАН. – СПб.: СПИИРАН, 2013.
2. Городецкий Ю. И. Функции чувствительности и динамика сложных механических систем. – Н.Новгород: ННГУ, 2006.
3. Юрескул А. Г. Идентификация параметров элементов комплекса полунатурного моделирования на основе функций чувствительности. Корабельные и бортовые многоканальные информационно-управляющие системы: Научно-технический сборник, УДК.681.327.11 – Выпуск №6. ОАО «Концерн «Гранит-Электрон», 2012.
4. Розенвассер Е. Н., Юсупов Р. М. Чувствительность систем автоматического управления. – М.: Наука, 1981.
5. Юрескул А. Г. Оценка отклонения параметров в процессе полунатурной отработки бортовой аппаратуры БПЛА. Корабельные и бортовые многоканальные информационно-управляющие системы: Научно-технический сборник, УДК.681.327.11 – Выпуск №6. ОАО «Концерн «Гранит-Электрон», 2012.
6. Шампайн Л. Ф. Решение обыкновенных дифференциальных уравнений с использованием MATLAB. – СПб.: Лань, 2009.
7. Кондрашин А.В., Хорьков В.И. Исследование и идентификация управляемых технических систем. – М.: ИспоСервис, 2000.
8. Демидович Б. П., Моденов В. П. Дифференциальные уравнения: Учебное пособие. 3-е изд., стер. – СПб.: Лань, 2008.
9. Жидков Е. Н., Вычислительная математика. – М.: Академия, 2010.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.