На рисунке 1 представлена общая схема теории чувствительности. Из нее видно, что теория чувствительности включает в себя методы получения функций и коэффициентов чувствительности и методы использования этих функций и коэффициентов, или, другими словами, решение прикладных задач теории чувствительности.
Для получения функций и коэффициентов чувствительности существует несколько методов, в том числе и интересующий нас метод – с помощью уравнений чувствительности.
Прикладные задачи, в свою очередь, делятся на:
· прямые задачи;
· обратные задачи;
· смешанные задачи.
Каждая из этих разновидностей задач включает в себя определенные подзадачи, такие, как:
· анализ устойчивости;
· контроль и диагностика;
· идентификация;
· оптимизация и другие.
На рисунке через Δα обозначена вариация вектора параметров системы, через Δy – вариация вектора состояния системы и через u – вектор функций (коэффициентов) чувствительности.
![]()
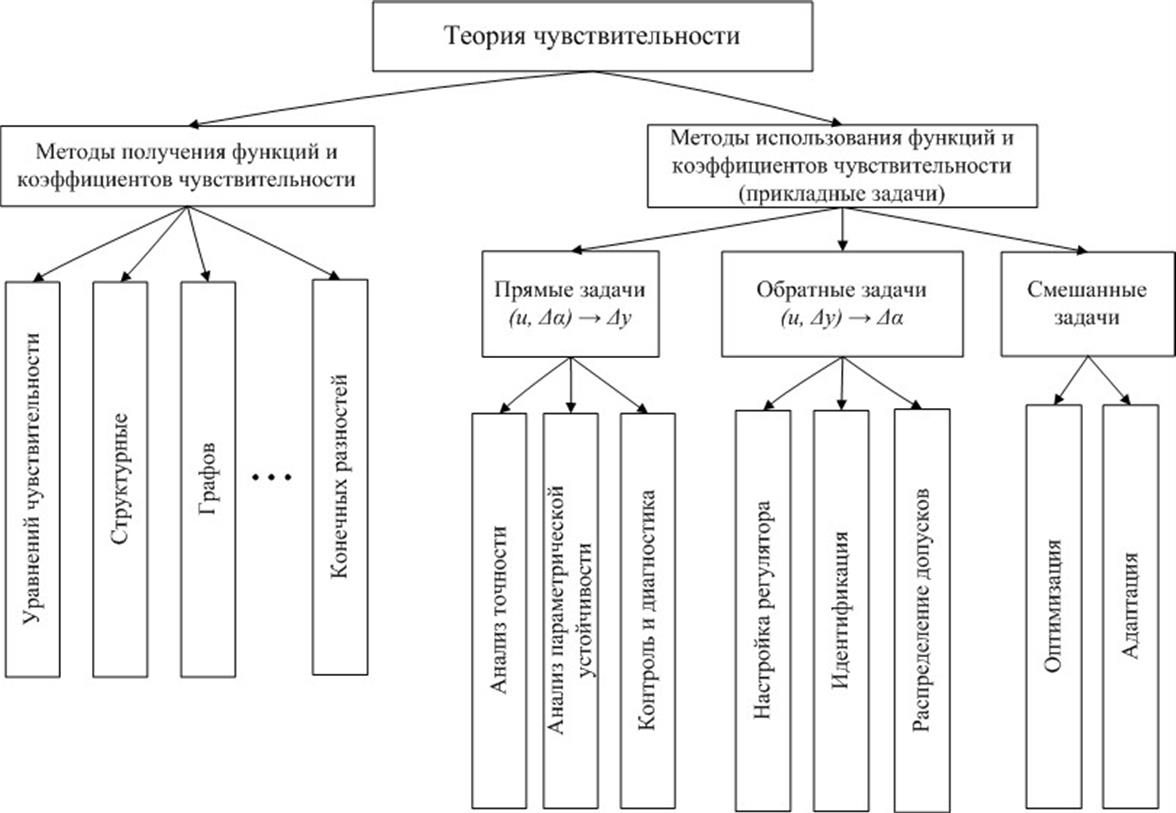 Рисунок 1 – Общая схема
теории чувствительности
Рисунок 1 – Общая схема
теории чувствительности
Имея функции чувствительности, становится возможным решать ряд задач анализа систем регулирования, подверженных влиянию параметрических возмущений. Кроме того, использование функций чувствительности делает возможной постановку некоторых задач синтеза систем управления, когда критерий оптимальности формулируется с учетом требований к нечувствительности системы. Параллельно с этим использование информации о функциях чувствительности является теоретической основой построения различных беспоисковых самонастраивающихся систем.
Методы теории чувствительности позволяют оценивать степень влияния параметрических возмущений на различные характеристики системы (переменные состояния, показатели качества и др.) и используются в качестве одной из основ современных методов синтеза робастных (грубых) систем, сохраняющих требуемое качество в условиях параметрических возмущений [1].
При проектировании и исследовании систем управления необходимо учитывать влияние параметрических возмущений на работу системы в целом и её отдельных компонент. Эффективным инструментом для подобного анализа является теория чувствительности, которая с помощью функций чувствительности позволяет оценить влияние отклонения параметров на работу системы [3].
Пусть исследуемая система задана в виде системы нелинейных обыкновенных дифференциальных уравнений:
![]()
![]() (1)
(1)
где ![]() – задающее воздействие;
– задающее воздействие;
![]() –
вектор параметров системы;
–
вектор параметров системы;
![]() –
вектор фазовых координат;
–
вектор фазовых координат;
![]() –
матрица выхода;
–
матрица выхода;
![]() –
вектор выходных координат системы;
–
вектор выходных координат системы;
![]() –
нелинейная вектор-функция, непрерывная по
–
нелинейная вектор-функция, непрерывная по ![]() ,
дифференцируемая по
,
дифференцируемая по![]() ;
;
![]() – начальное условие;
– начальное условие;
![]() – начальный и
конечный моменты времени расчета.
– начальный и
конечный моменты времени расчета.
Под чувствительностью систем управления принято понимать зависимость их свойств от изменения параметров [4].
Вектор
состояния модели объекта является вектор функцией параметров α
и t:![]() .
.
Предполагаем,
что для решения ![]() выполняются условия единственности
решения, а условие дифференцируемости
выполняются условия единственности
решения, а условие дифференцируемости ![]() по
параметрам α и t
существенно
определяет получение уравнений чувствительности.
по
параметрам α и t
существенно
определяет получение уравнений чувствительности.
Пусть![]() – вектор решения
системы при номинальном векторе параметров
– вектор решения
системы при номинальном векторе параметров ![]() , а
, а
![]() (2)
(2)
– решение
системы при измененном векторе параметров ![]() .
Раскладывая возмущенное решение
.
Раскладывая возмущенное решение![]() в
ряд Тейлора в окрестности номинальных значений параметров и ограничиваясь двумя
членами разложения, получаем:
в
ряд Тейлора в окрестности номинальных значений параметров и ограничиваясь двумя
членами разложения, получаем:
![]() (3)
(3)
Тогда матрица чувствительности определяется равенством:
![]() (4)
(4)
Функцией
чувствительности по параметру ![]() называется i-ый
столбец матрицы чувствительности
называется i-ый
столбец матрицы чувствительности ![]() .
.
Также функции чувствительности могут быть определены известным матричным уравнением, которое называется уравнением чувствительности:
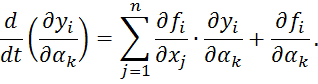
С
учетом (4), произведя замену 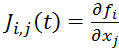 и
и ![]() , получим:
, получим:
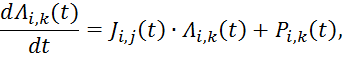
![]() (5)
(5)
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.