Параметрическая идентификация модели электрогидравлического рулевого привода методами теории чувствительности, страница 5

Существующие методы решения этой задачи идентификации [7] (под идентификацией понимается процесс построения адекватных математических моделей исследуемых объектов) требуют, чтобы были измеряемы все переменные, входящие в уравнения, причем расстояние между дискретами должно быть таким, чтобы можно было с достаточной степенью точности вычислять соответствующие производные и интегралы. Кроме того, широко известный метод – метод модулирующих функций [8], применим лишь к дифференциальным уравнениям, в которые искомые параметры и производные от переменных входят линейно.

Также существует метод решения задачи идентификации, не требующий обязательного выполнения указанных выше условий, т.е. при неполной наблюдаемости переменных линейного и нелинейного объекта. Под неполной наблюдаемостью переменных понимается то, что экспериментальные данные получены в дискретные моменты времени. Данный метод основан на использовании в качестве аппроксимирующих операторов ОДУ и хорошо известный среди специалистов, занимающихся проблемами идентификации и оценивания параметров математических моделей процессов и объектов, стандартными алгоритмами чувствительности.

Содержательная сущность задачи аппроксимации экспериментальных данных [9] заключается в том, чтобы, используя ту или иную вещественную функцию одной вещественной переменной, описать зависимость одной переменной от другой и сделать это таким образом, чтобы точность полученного описания удовлетворяла предъявляемым к ней требованиям.

Анализируя данную задачу с математической точки зрения, нетрудно видеть, что она является существенно неопределенной, прежде всего потому, что в настоящее время известно весьма значительное множество вещественных функций одной вещественной переменной, используя которые можно добиться желаемой точности математического описания обсуждаемой нами зависимости. В частности, вполне успешно это можно сделать, если при решении рассматриваемой задачи воспользоваться алгебраическими, тригонометрическими, экспоненциальными, логарифмическими и т.п. полиномами; дробно-рациональными функциями одной вещественной переменной [9] или решениями дифференциальных уравнений. Ещё одной причиной существенной неопределенности данной задачи является то, что для количественной оценки точности математического описания экспериментальных данных можно воспользоваться многими, как уже известными, так и вновь предложенными количественными характеристиками погрешности данного описания. Одна их таких характеристик будет рассмотрена далее.

Как вытекает из изложенного в предыдущем абзаце, для получения математически корректной постановки рассматриваемой задачи, необходимо, во-первых, выбрать класс функций, заданных с точностью до некоторого набора параметров, изменяя которые можно влиять на точность получаемой аппроксимации экспериментальных данных. Во-вторых, задать какую-либо конкретную количественную характеристику погрешности данного описания. Учитывая отмеченные причины недоопределенности рассматриваемой задачи и задавшись целью устранить данные причины, чтобы в итоге получить корректно поставленную математическую задачу, сформируем задачу количественного описания экспериментальных данных, полученных в результате проведенных нами измерений, базируясь на следующих трех положениях.

Для количественной оценки погрешностей описания имеющихся измеренных значений функциями вида (2), будем использовать функционал, заданный видом:

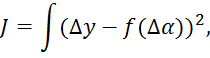
где . Тогда получим:

,                                                     (8)

,

, где  измененные значения параметров;

 начальные (неизмененные) значения параметров;

 значение функции при измененных параметрах;

 значение функции при начальных параметрах.

Необходимо подобрать значения неизвестных параметров так, чтобы решение (2) доставляло минимум функционалу J, определяемому равенством (8), и, соответственно, удовлетворяло условию:

.                                             (9)

С учетом (3) получаем:

(10)

Приступим теперь к формированию системы уравнений относительно поправок . Для этого воспользуемся функционалом J, заданным равенством (9), и соотношением (10). Подставляя вычисленные значения функций  и ФЧ Λ в соотношение (10), а затем в правую часть равенства (9), получим, что: