Параметрическая идентификация модели электрогидравлического рулевого привода методами теории чувствительности, страница 3

где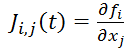  – матрица частных производных по переменным состояния или якобиан исследуемой системы (1);

  – матрица частных производных по параметрам системы.

Таким образом, функции чувствительности могут быть найдены посредством решения системы дифференциальных уравнений порядка n´m. Получение и решение такой системы уравнений является достаточно трудоемкой задачей, особенно для систем высокого порядка, и требует применения приближенных численных методов. Кроме того, на практике часто интерес представляет оценка чувствительности только некоторых переменных состояния, например, выходного сигнала, сигнала ошибки и т.п.

В простейших случаях, когда удается получить в аналитической форме законы изменения переменных состояния для основного движения, функции чувствительности могут быть получены непосредственно их дифференцированием.

2  Модель рулевого привода

Из всех элементов системы угловой стабилизации (СУС), наибольшей инерционностью обладает рулевой привод (РП), что позволяет в качестве инерционности системы стабилизации рассматривать инерционность рулевого привода.

Рулевой привод – следящая система с жесткой обратной связью.

Основным исполнительным элементом рулевого привода является рулевая машинка. Рулевые машинки бывают нескольких типов:

·  электрическая (электродвигатель);

·  электропневматическая;

·  электрогидравлическая.

В системах управления ЛА чаще всего используются электрогидравлические рулевые машинки, связано это, прежде всего, с необходимостью развивать большие крутящие моменты и требованиями по быстродействию.

Рулевой привод включает в себя (рисунок 2):

·  усилитель рулевого привода;

·  рулевую машинку;

·  цепь обратной связи.

Рисунок 2 – Функциональная схема рулевого привода

Добротность РП  – произведение коэффициентов усиления в замкнутом контуре:

,

(

где     – коэффициент усиления рулевого тракта;

 – коэффициент усиления (передачи) рулевой машинки;

   – коэффициент усиления в цепи обратной связи.

В большинстве случаев рулевой привод имеет жесткую обратную связь, кроме того рабочие режимы моделирования, как правило, обеспечивают квазилинейное движение, при котором нелинейностями типа «насыщение» можно пренебречь [5].

Учитывая подобные допущения схема рулевого привода может быть представлена последовательностью линейных динамических звеньев (рисунок 3).

 

Рисунок 3 – Линеаризованная схема рулевого привода

Линеаризованный рулевой привод может быть описан следующей системой линейных дифференциальных уравнений:

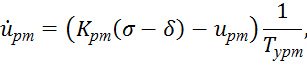
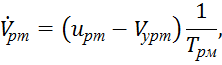
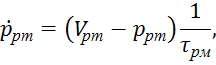
                                                             (6)

Перепишем систему (6) в следующем виде:

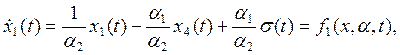
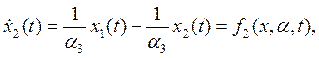
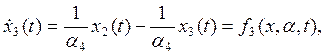
где – вектор переменных состояния;

– вектор параметров системы;

– управляющий сигнал, вырабатываемый системой управления.

Для расчета функций чувствительности математической модели рулевого привода определим матрицы и . В итоге получим:

,

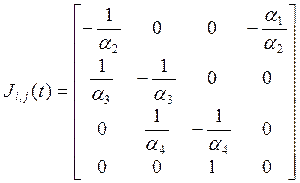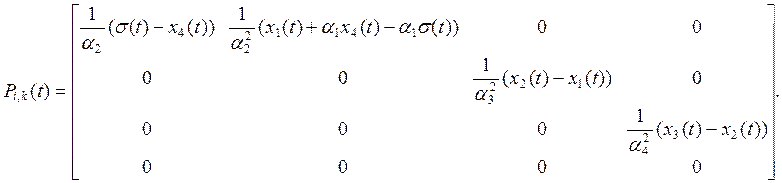
Подставляя полученные матрицы и в уравнение чувствительности (5) и раскрывая матричное уравнение получаем систему дифференциальных уравнений, определяющих элементы матрицы чувствительности .

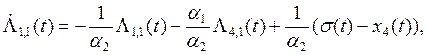
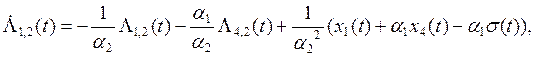
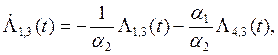
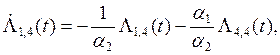
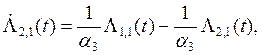
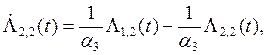
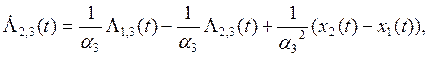
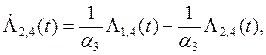
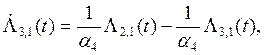
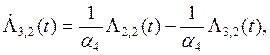
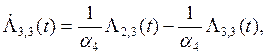
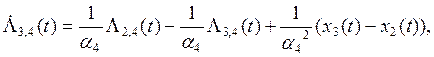
                                                        (7)

3  Программная реализация математической модели чувствительности электрогидравлического рулевого привода

В общем виде модель получения матрицы чувствительности может быть представлена в виде схемы, представленной на рисунке 4.

 

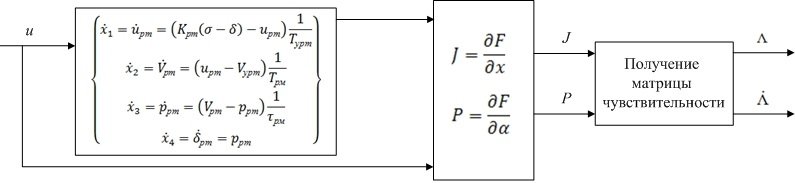
Рисунок 4 – Общая схема алгоритма чувствительности

Беря частные производные  и , получаем матрицы , . В свою очередь, блок получения матрицы чувствительности представляется в виде схемы, представленной на рисунке 5.

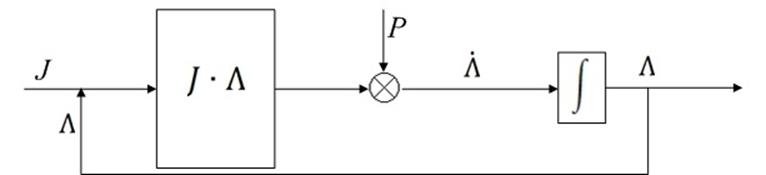
Рисунок 5 – Схема вычисления матрицы Λ