Эта схема реализует уравнение (5). Результатом работы схемы, представленной на рисунке 4, будет система уравнений (7). Далее, в среде имитационного моделирования MATLAB/Simulink реализовывался данный алгоритм и выполнялась подстановка чисел, в результате чего было получено численное решение системы дифференциальных уравнений (7) [6]. Схема реализации представлена на рисунке 6.
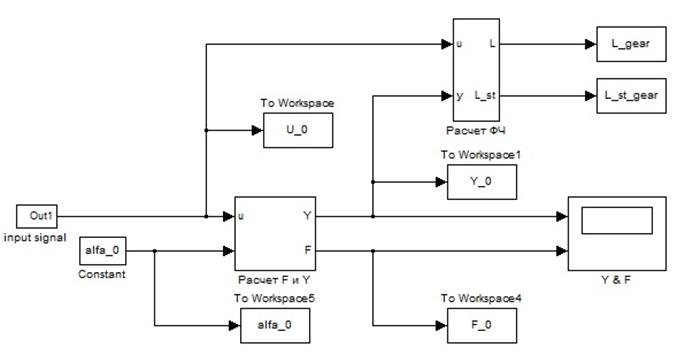
Рисунок 6 – Программная реализация алгоритма
Расчет системы дифференциальных уравнений рулевого привода производится в подсистеме, представленной на рисунке 7.
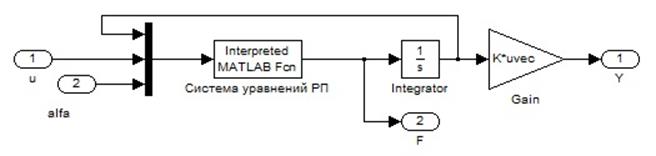
Рисунок 7 – Расчет систему ДУ
Матрицы
![]() ,
, ![]() и
и ![]() также получены программным путем в
среде MATLAB/Simulink
(рисунок 8).
также получены программным путем в
среде MATLAB/Simulink
(рисунок 8).
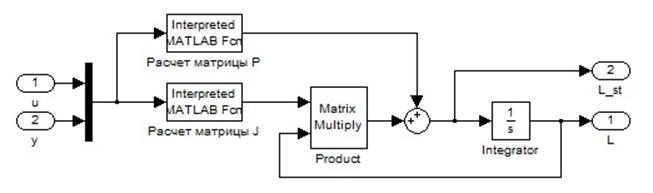
Рисунок 8 – Расчет матриц P, J, Λ
На рисунках 9 и 10 представлены графики нелинейной вектор-функции F(t) и вектора выходных координат системы Y(t).
При синусоидальном входном воздействии (рисунок 9).
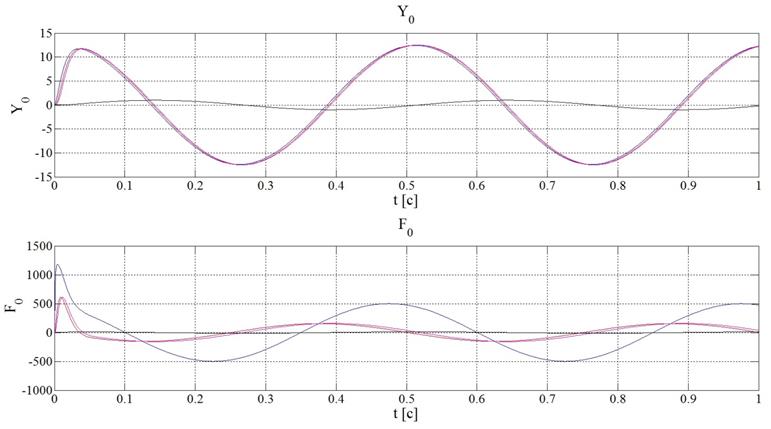
Рисунок 9 – Графики F(t) и Y(t) при синусоидальном задающем воздействии
При задающем воздействии, равном константе (рисунок 10).
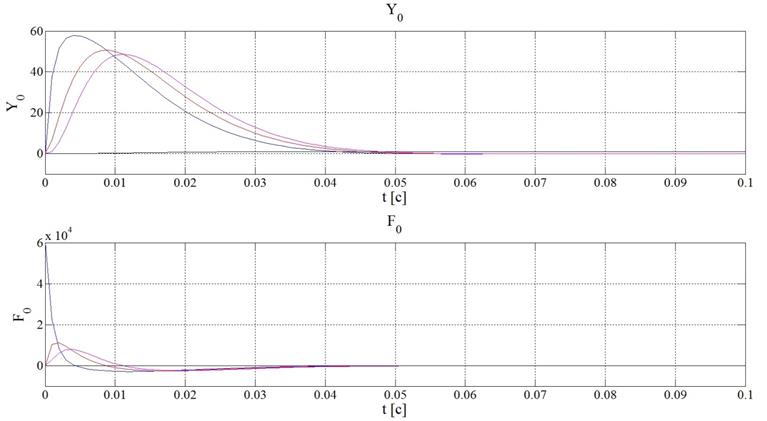
Рисунок 10 – Графики F(t) и Y(t) при задающем воздействии, равном константе
Функции чувствительности математической модели рулевого привода при синусоидальном задающем воздействии представлены на рисунке 11.
Функции чувствительности математической модели рулевого привода при задающем воздействии, равном константе, представлены на рисунке 12.
![]()
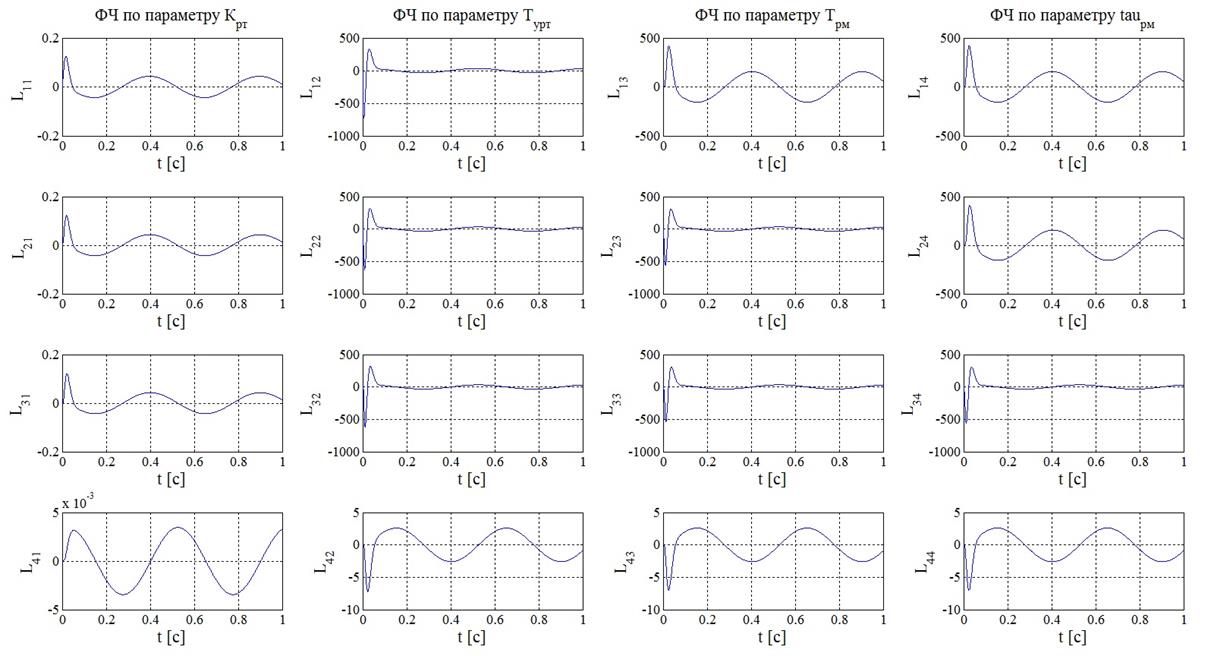
Рисунок 11 – Функции чувствительности математической модели РП
![]()
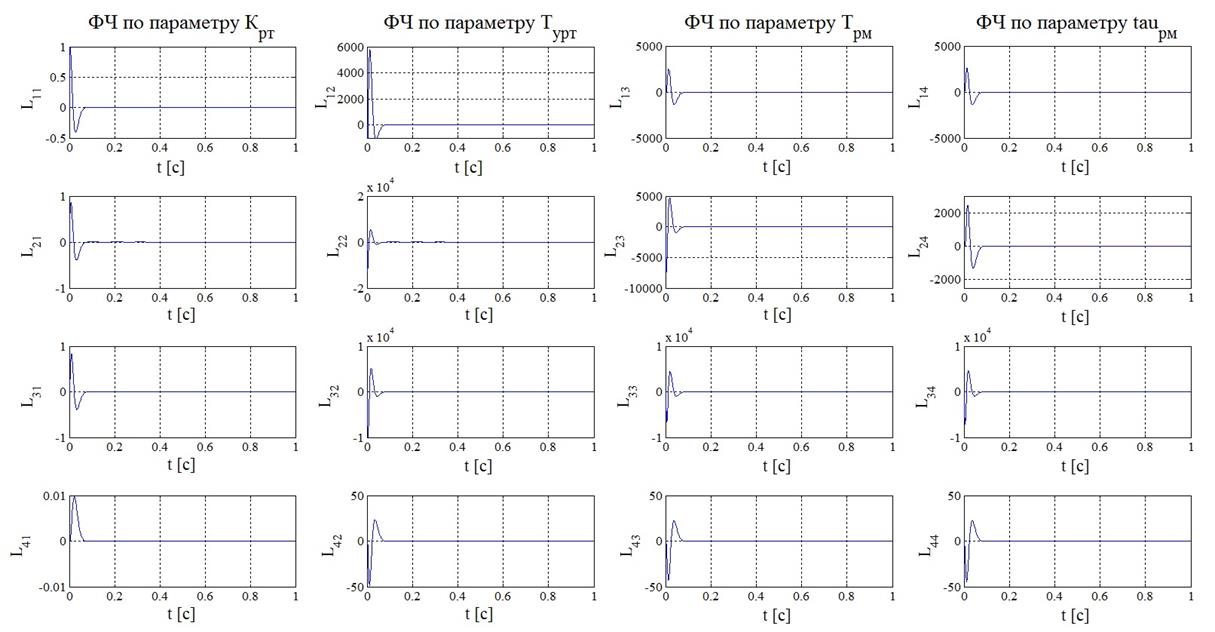
Рисунок 12 – Функции
чувствительности математической модели РП
Идентификация объектов в настоящее время является обязательным элементом и наиболее сложной стадией выполнения ряда прикладных проектов. Оперативное и адекватное решение ее проблем создает необходимые условия эффективного практического использования математических методов и сложных наукоемких технологий. Разработка методов и алгоритмов идентификации приобретает в настоящее время исключительно важное значение для фундаментальной науки. Развитие теории идентификации в классическом направлении сейчас также актуально и практически значимо, как и в 50-е годы XX века, когда она зарождалась под влиянием насущных проблем практики. Постоянная необходимость в оптимизации процесса решения практических проблем за счет рациональной идентификации стимулирует прогресс теории в классическом направлении. В связи с этим по-прежнему актуальны для фундаментальной науки такие области исследования, как математические методы параметрической и непараметрической идентификаций, математическая теория структурной идентификации, математическое моделирование систем, математические проблемы управления с оперативным идентификатором, методологии идентификации при известной адекватной математической постановке практической проблемы.
Для решения многих классов задач управления и идентификации используется широко известный среди специалистов по автоматическому управлению и специалистов, занимающихся проблемами идентификации исследуемых процессов, явлений, объектов и т.п., алгоритм чувствительности (будем называть его базовым или стандартным). На его основе можно с единых позиций подходить к вопросам идентификации различных классов динамических объектов (непрерывных, дискретных, сосредоточенных, распределенных и др.), а также решать краевые задачи алгоритмического конструирования оптимальных регуляторов.
Будем рассматривать случай, когда из предварительного анализа исследуемого процесса удается составить его модель в виде системы ОДУ с точностью до параметров, которые необходимо определить на основе наблюдений некоторых переменных процесса в дискретных точках пространственной и временной координат.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.