Машиностроение \ Системы управления летательными аппаратами

Параметрическая идентификация модели электрогидравлического рулевого привода методами теории чувствительности, страница 6

                                    (11)

Таким образом, мы получили функционал, который можно использовать для количественной оценки погрешностей описания имеющихся у нас измеренных значений  функциями, являющимися решениями дифференциального уравнения.

Как видно из равенства (11), функционал J удовлетворяет равенству , т.е. является явно заданной и положительно определенной функцией поправок . Для этого, как известно из математического анализа, необходимо и достаточно продифференцировать функционал J по вектору поправок  и приравнять полученные при этом частные производные к нулю. Выполнив данные операции над функционалом J, получим:

Если выполнить все необходимые и вполне очевидные арифметические операции, то данной системе уравнений можно придать следующий, предельно компактный и традиционный в линейной алгебре вид:

где:

а)   

b).                                                 (12)

Здесь  – квадратная матрица порядка n+1. Как видно из (12b), эта матрица является симметричной.

Полученная система является системой линейных алгебраических уравнений относительно вектора поправок . Решение , как известно, определяется равенством:

Подставляя известные нам величины, получим:

                                        (13)

В общем виде схема идентификации может быть представлена в виде блок-схемы, представленной на рисунке 13.

uT ,Λ^T Λ ,Λ^T Δy ,∫ ,∫ ,∫▒( Λ^T Λ)^(-1) ,[∫▒〖(Λ^T Λ〖)dt]〗^(-1) 〗 ∫▒Λ^T Δydt,Λ,∆y ,Δα
 


Рисунок 13 – Общая схема реализации идентификации

Решение уравнения (13) получено в среде имитационного моделирования MATLAB/Simulink. Схема реализации представлена на рисунке 14.

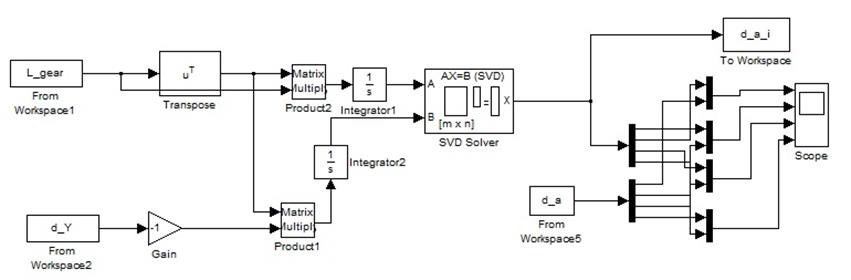
ident_sim.jpg

Рисунок 14 – Программная реализация уравнения (13)

Результаты идентификации при  и синусоидальном задающем воздействии представлены на рисунке 15.

Теперь проведем оценку погрешности идентификации параметров, используя следующий критерий оценки:

                                                  (14)

Также проведем оценку, обратившись к функционалу (11), который необходимо было минимизировать. Для наглядности рассмотрим как весь функционал целиком, так и входящие в него элементы.

Примем:

(15)

Тогда:

                                         (16)

.                           (17)

Реализовав оценивание ошибки с помощью данных критериев в среде имитационного моделирования MATLAB/Simulink, доработав схему, предназначенную для решения уравнения (13), получим модель, представленную на рисунке 16.

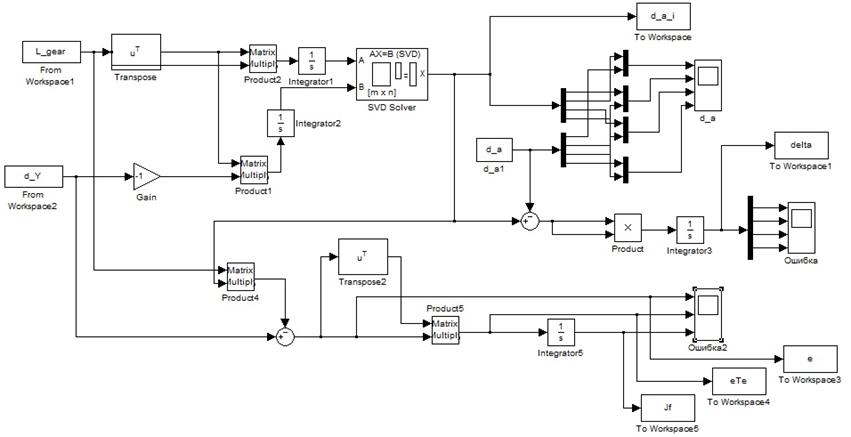
ident_vs_delta.jpg

Рисунок 16 – Программная реализация уравнения (13) с критериями оценки


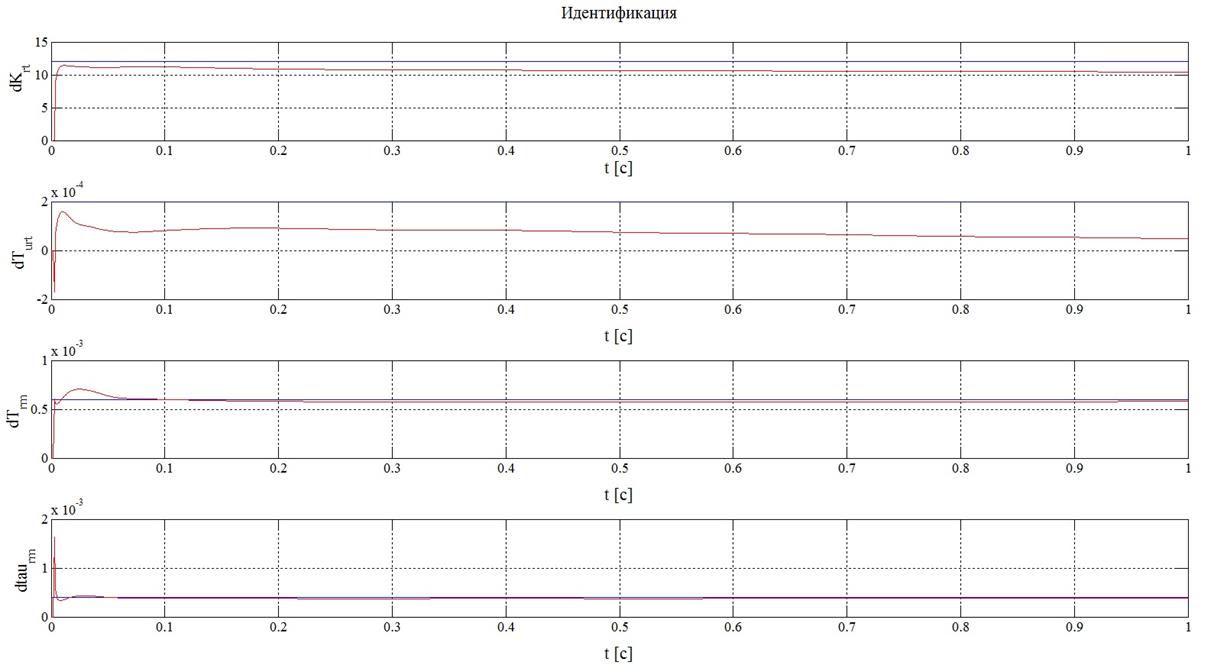
27ident_sin_+20.jpg

Рисунок 15 – Результаты идентификации при синусоидальном задающем воздействии и



На рисунке 17 представлены результаты проведения оценки точности идентификации, проведенной с помощью критерия (14).

Результаты оценки, проведенной с помощью критериев (15), (16) и (17) представлены на рисунке 18, где:

·  1-й график – критерий e;

·  2-й график – критерий eTe;

·  3-й график – критерий Jf.


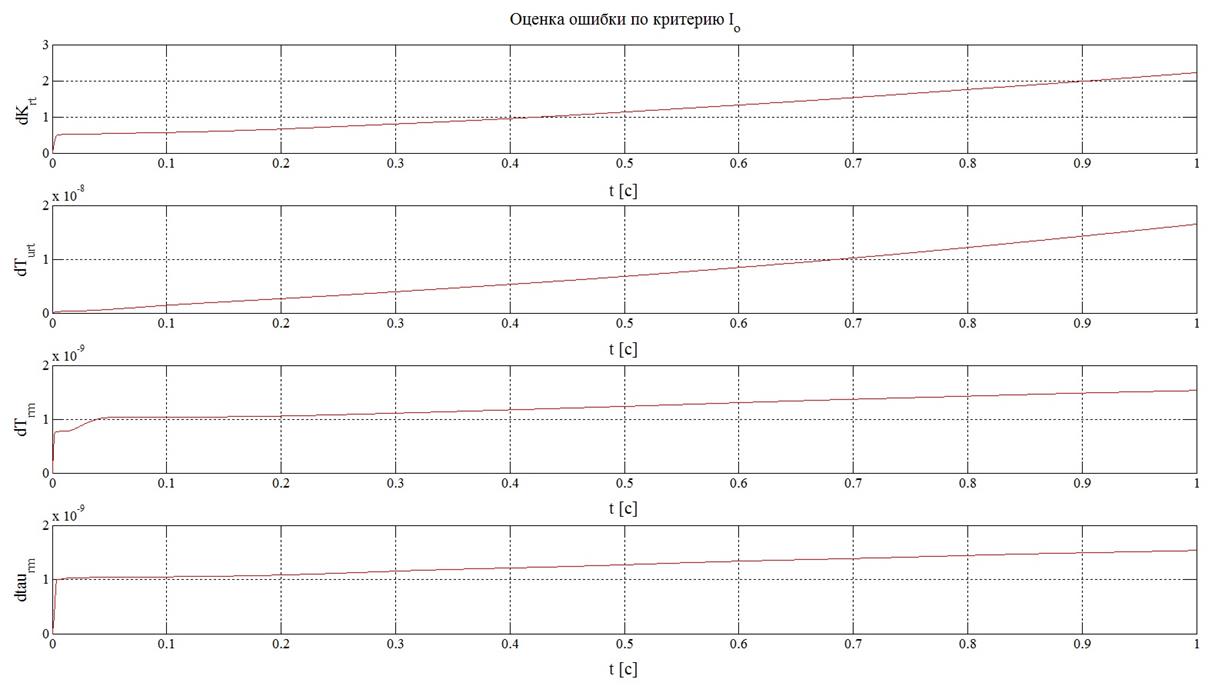
29delta_io_sin_+20.jpg

Рисунок 17 – Результаты оценки с помощью критериев (14) при синусоидальном задающем воздействии и



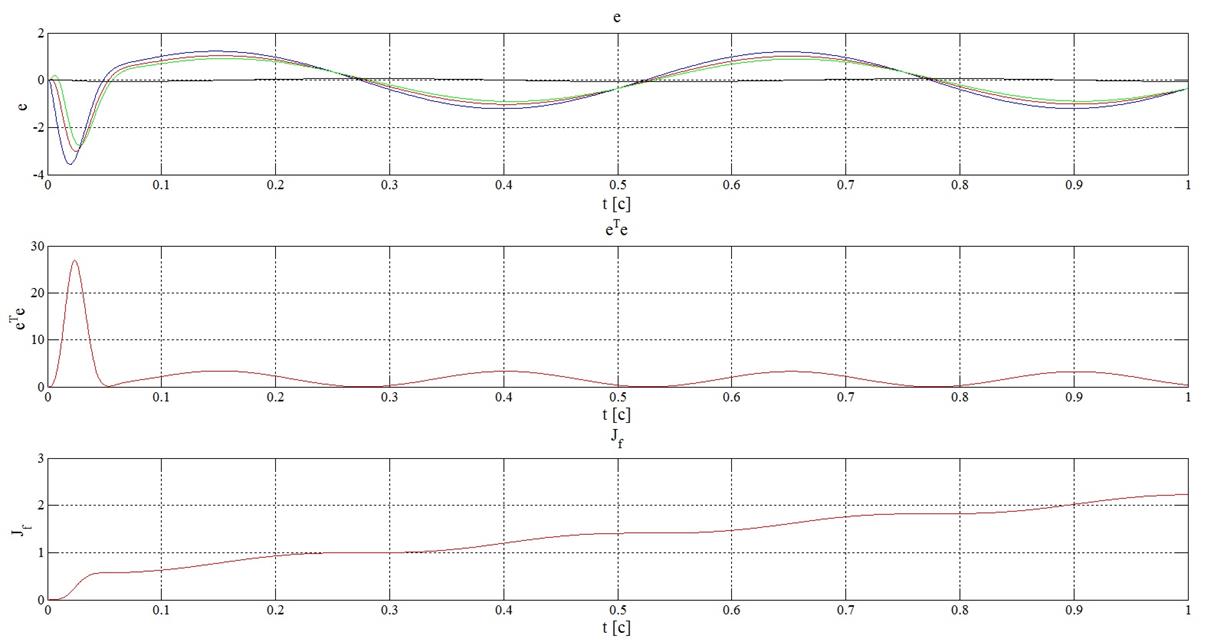
30delta_e_sin_+20.jpg

Рисунок 18 – Результаты оценки с помощью критериев (14), (16) и (17) при синусоидальном задающем воздействии и


6  Идентификация параметрических возмущений при различных входных сигналах

Теперь в качестве задающего воздействия будем использовать константу. Результаты идентификации представлены на рисунке 19.

Результаты оценки точности с помощью критерия (14) – на рисунке 20.

Результаты, полученные с помощью критериев (15), (16) и (17) – на рисунке 21, где:

·  1-й график – критерий e;

·  2-й график – критерий eTe;

·  3-й график – критерий Jf.

Далее изменим значение , изменив значение  на .  Измерения проводим для двух видов задающего воздействия: синусоидальном и равному константе.

Результаты измерений при синусоидальном задающем воздействии представлены ниже. На рисунке 22 изображены графики идентификации параметра . Рисунок 23 показывает графики оценки погрешности идентификации с помощью критерия (14), а рисунок 24 – с помощью критериев (15), (16) и (17).

В завершении всего, проведем те же измерения при задающем воздействии, равном константе. Результаты измерений представлены ниже. На рисунке 25 изображены графики идентификации параметра . Рисунок 26 показывает графики оценки погрешности идентификации с помощью критерия (14), а рисунок 27 – с помощью критериев (15), (16) и (17).

Во время данных исследований в функционале (11) на место INподставлялась квадратная матрица с единичной диагональю:

.

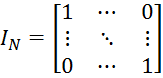Анализируя полученные графики, мы видим, что с течением времени ошибка идентификации увеличивается, что говорит о несовершенстве используемого алгоритма идентификации.

Скачать файл