Методы решения систем линейных алгебраических уравнений (Лабораторная работа № 3), страница 7

D_n2  = Δ₃/Δ = - 25519849,3/ - 4727249,8 = 5,4(кг/с)

9.  Решаем СЛАУ методом Гаусса:

39,4G’_ок  - 2182,2D_n1  = 44

G’_ок  - D_n1  - D_п2  = 115,44

559,5G’_ок  -  619,7D_n1 - 2764,4D_п2 = 52540,8

- D_п2  + G’_ок  - D_n1  = 115,44

- 2764,4D_п2 + 559,5G’_ок  -  619,7D_n1 = 52540,8

39,4G’_ок  - 2182,2D_n1  = 44

Умножим первое уравнение на а₂₁ / а₁₁ и вычтем его из второго уравнения:

- D_п2  + G’_ок  - D_n1  = 115,44

-2204,9G’_ок  + 2144,7D_n1 = - 266581,5

39,4G’_ок  - 2182,2D_n1  = 44

Умножим второе уравнение на а₃₂ / а₂₂ и вычтем его из третьего уравнения:

- D_п2  + G’_ок  - D_n1  = 115,44

-2204,9G’_ок  + 2144,7D_n1 = - 266581,5

- 2220,5D_n1  = - 4807,6

Отсюда,

D_n1  = - 4807,6/-2220,5 = 2,17(кг/с)

- D_п2  + G’_ок    = 117,61

2204,9 G’_ок  = 271235,5

G’_ок = 271235,5/ 2204,9 = 123,01(кг/с)

D_п2  = 5,4(кг/с)

Заключение: при решении системы линейных алгебраических уравнений ответы получились одинаковыми (с учётом погрешностей).

Билет№19

Лабораторная работа №3: Методы решения систем линейных алгебраических уравнений.

Цель: ознакомится с методами численного решения систем линейных алгебраических уравнений. Получить навыки в разработке алгоритмов и программ реализующих методы решения систем линейных алгебраических уравнений. Закрепить знания по использованию пакета прикладных программ на примерах расчёта теплообменников ТЭС.

Дано: Р_п = 0,45МПа; t_n =200 ^0C; G”_ок =150кг/с; Д_д = 5кг/с; t_д =160 ^0C; Д_д2 =7кг/с; t_д2 =120 ^0C;

Р_ок = 1,3МПа; t_ок =25 ^0C.

Найти: Д_п; G_ок; G’_ок ; t’_ок; t”_ок; t’”_ок.

Составляем уравнения балансов:

Д_п(h_n – h’_n) = G”_ок(ŧ’”_ок – ŧ_cn)

Д_п(h’_n – ŧ’_д) + Д_д(ŧ_д – ŧ’_д) = G”_ок(ŧ_cn – ŧ”_ок)

Д_п + Д_д + G’_ок = G”_ок

(Д_п + Д_д) ŧ’_д + G’_ок ŧ’_ок = G”_ок ŧ”_ок

Д_д2 + G_ок = G’_ок

Д_д2ŧ_д2 + G_ок ŧ_ок = G’_ок ŧ’_ок

Сложим четвёртое с последним и третье с пятым уравнением:

Д_п(h_n – h’_n) = G”_ок(ŧ’”_ок – ŧ_cn)

Д_п(h’_n – ŧ’_д) + Д_д(ŧ_д – ŧ’_д) = G”_ок(ŧ_cn – ŧ”_ок)

Д_п + Д_д + Д_д2 + G_ок = G”_ок

(Д_п + Д_д) ŧ’_д + Д_д2ŧ_д2 + G_ок ŧ_ок = G”_ок ŧ”_ок

Сложим второе с последним уравнением:

Д_п(h_n – h’_n) = G”_ок(ŧ’”_ок – ŧ_cn)

Д_пh’_n  + Д_дŧ_д  + Д_д2ŧ_д2 + G_ок ŧ_ок = G”_ок ŧ_cn

Д_п + Д_д + Д_д2 + G_ок = G”_ок

Находим известные величины:

h_п = f(Р_n; t_n) = f(0,45МПа; 200 ⁰C ) =  2848,8 (кДж/кг).

h'_п = f(Р_n; t_s( Р_n)  + 10 – 15 ⁰C) = f(0,45МПа; 147,9 + 12 ⁰C ) = 2751,9 (кДж/кг).

h_сп =  (t_s( Р_n)  - Q) · С_в = (147,9 - 5 ⁰C ) · 4,19 = 598,8(кДж/кг).

ŧ_д  = t_д · С_в = 160 · 4,19 = 670,4 (кДж/кг).

ŧ_д2  = t_д2 · С_в = 120 · 4,19 = 502,8 (кДж/кг).

ŧ_ок = f(Р_ок; t_ок) = f(1,3МПа; 25 ⁰C ) =  106 (кДж/кг).

Подставляем найденные величины в систему уравнений;

96,9Д_п – 150 ŧ’”_ок  = – 89820

2751,9Д_п  + 106G_ок  = 82948,4

Д_п + G_ок = 138

10.  Решаем данную систему уравнений методом Крамера:

Составляем матрицу:

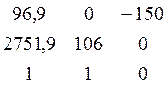
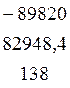А =   В =         Х =

Находим главный определитель

Δ = 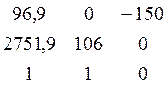   = - 396885

Находим второстепенные определители

Δ₁ = 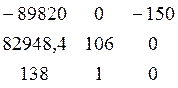   = - 10248060

Δ₂ = 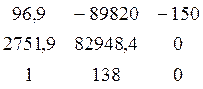   = - 44522070

Δ₃ = 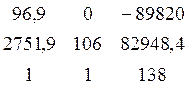   = - 244274984,8

Находим искомые величины

Д_п = Δ₁/Δ = - 10248060/-396885 = 25,82 (кг/с)

G_ок = Δ₂/Δ = - 44522070/-396885 = 112,18 (кг/с)

ŧ’”_ок = Δ₃/Δ = - 244274984,8/-396885 = 615,5 (кДж/кг)

2.      Решаем СЛАУ методом Гаусса:

Д_п + G_ок = 138

2751,9Д_п  + 106G_ок  = 82948,4

96,9Д_п – 150 ŧ’”_ок  = – 89820

Умножим первое уравнение на а₂₁/а₁₁ и вычтем его из второго уравнения

Д_п + G_ок = 138

- 2645,9G_ок  = - 296813,8

96,9Д_п – 150 ŧ’”_ок  = – 89820

Отсюда,

G_ок  = 112,18

Д_п = 138 – 112,18

96,9Д_п – 150 ŧ’”_ок  = – 89820

G_ок  = 112,18

Д_п = 25,82

– 150 ŧ’”_ок  = – 92321,96

G_ок  = 112,18

Д_п = 25,82

ŧ’”_ок  = 615,5

Найдём t’”_ок

t’”_ок = ŧ’”_ок /С_в = 615,5/4,19 = 146,9 (⁰С)

Найдём остальные недостающие искомые величины

G’_ок = Д_д2 + G_ок = 7 + 112,18 = 119,18 (кг/с)

ŧ’_ок = (Д_д2ŧ_д2 + G_ок ŧ_ок)/G’_ок = (7 · 502,8 + 112,18 · 106)/ 119,18 = 129,3 (кДж/кг)

t’_ок = ŧ’_ок /С_в = 129,3/4,19 = 30,86 (⁰С)

ŧ”_ок =((Д_п + Д_д)ŧ’_д + G’_ок ŧ’_ок)/G”_ок = ((25,82 + 5) · 619,7 + 119,18 · 129,3)/150 = 230,1(кДж/кг)

t”_ок = ŧ”_ок /С_в = 230,1/4,19 = 54,9 (⁰С)

Заключение: при решении СЛАУ методами Крамера и Гаусса искомые величины получились одинаковыми.