Найдём главный определитель.
1 1
D = = - 2335
2903,2 568,2
Найдём второстепенные определители.
103,73 1
D1 = = - 18342,1
77281,5 568,2
1 103,73
D2 = = - 223867,4
2903,2 77281,5
Найдём искомые величины.
Dn1 = D1 / D = - 18342,1 / - 2335 = 7,86(кг/с)
Gок = D2 / D = - 223867,4 / - 2335 = 95,87(кг/с)
Найдём Dn:
Dn = Dn1 + Dn2 = 6,27 + 7,86 = 14,13 (кг/с).
2. Решаем данную систему уравнений методом Гаусса:
Dn1 + Gок = 103,73
2903,2Dn1 + 568,2Gок = 77281,5
Умножим первое уравнение на а21 / а11 и вычтем его из второго уравнения:
Dn1 + Gок = 103,73
0 - 2335Gок = - 223867,4
Отсюда,
Dn1 + Gок = 103,73
Gок = 95,87
Dn1 = 103,73 - 95,87
Gок = 95,87
Dn1 = 7,86
Gок = 95,87
Ответ: Dn = 14,13 (кг/с); Gок = 95,87 (кг/с); t''пв = 192,4 0C.
Заключение: при решении системы линейных алгебраических уравнений ответы получились одинаковыми.
Билет № 7
Лабораторная работа №3: Методы решения систем линейных алгебраических уравнений.
Цель: ознакомится с методами численного решения систем линейных алгебраических уравнений. Получить навыки в разработке алгоритмов и программ реализующих методы решения систем линейных алгебраических уравнений. Закрепить знания по использованию пакета прикладных программ на примерах расчёта теплообменников ТЭС.
Дано: Рn1 = 0,5 МПа; tn1 = 205 0C; Рn2 = 0,3 МПа; tn2 = 155 0C; Dд = 2 кг/с; tд = 160 0C; Gок = 95 кг/с; Рок = 1,2 МПа; tок = 60 0C;
Найти: D n1; D n2; Gсм; tсм.
Составляем уравнения балансов:
Dn1 (hп1 – ћд1) + Dд (ћд – ћд1) = Gсм ( ћ''ок – ћсм )
Dn1 + Dn2 + Dд + Gок = Gсм
(Dn1 + Dn2 + Dд )ћд2 + Gокћ'ок = Gсмћсм
Dn2 (hп2 – ћд2) + (Dn1 + Dд ) (ћд1 – ћд2) = Gок ( ћ'ок – ћок )
Сложим первое и третье уравнение:
Dn1 (hп1 – ћд1 + ћд2) + Dд (ћд – ћд1 + ћд2) + Dn2ћд2 + Gокћ'ок = Gсм ћ''ок
Dn1 + Dn2 + Dд + Gок = Gсм
Dn2 (hп2 – ћд2) + (Dn1 + Dд ) (ћд1 – ћд2) = Gок ( ћ'ок – ћок )
Найдём известные величины:
hп1 = f(Рn1; tn1) = f(0,5МПа; 205 0C ) = 2857,6 (кДж/кг).
hп2 = f(Рn2; tn2) = f(0,3МПа; 155 0C ) = 2752,1 (кДж/кг).
ћд1 = h’( Рn1) = 640,14 (кДж/кг).
ћд2 = h’( Рn2) = 561,5 (кДж/кг).
ћд = tд · Св = 160 · 4,19 = 670,4(кДж/кг).
ћок = f(Рок; tок) = f(1,2МПа; 60 0C ) = 252,1 (кДж/кг).
h'ок = f(Рn2; ts( Рn2) - Q) = f(0,3МПа; 133,54 - 5 0C ) = 540,1 (кДж/кг).
h''ок = f(Рn1; ts( Рn1) - Q) = f(0,5МПа; 151,84 - 5 0C ) = 618,6 (кДж/кг).
Подставляем найденные величины в систему уравнений:
2779Dn1 + 561,5Dn2 – 618,6Gсм = - 52493
Dn1 + Dn2 – Gсм = - 97
78,6Dn1 + 2190,6Dn2 = 27202,7
3. Решаем данную систему уравнений методом Крамера:
Составляем матрицу:
А =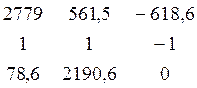 
В
= 
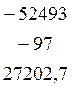Х = 
Найдём главный определитель:
D = 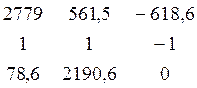= 4737060,3
Находим второстепенные определители:
D1 =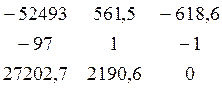 
= 18007308,9
D2 =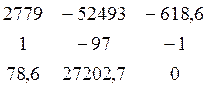 
= 58178332,8
D3 =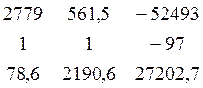 
= 535680490,8
Находим искомые величины:
Dn1 = D1 / D = 18007308,9 / 4737060,3 = 3,8 (кг / с)
Dn2 = D2 / D = 58178332,8 / 4737060,3 = 12,28 (кг / с)
Gсм = D3 / D = 535680490,8 / 4737060,3 = 113,08 (кг / с)
4. Решаем систему уравнений методом Гаусса:
– 618,6Gсм + 2779Dn1 + 561,5Dn2 = - 52493
– Gсм + Dn1 + Dn2 = - 97
78,6Dn1 + 2190,6Dn2 = 27202,7
Умножим первое уравнение на а21 / а11 и вычтем его из второго уравнения:
– 618,6Gсм + 2779Dn1 + 561,5Dn2 = - 52493
– 3,4924Dn1 + 0,0923Dn2 = - 12,1423
78,6Dn1 + 2190,6Dn2 = 27202,7
Умножим второе уравнение на а32 / а22 и вычтем его из третьего уравнения:
– 618,6Gсм + 2779Dn1 + 561,5Dn2 = - 52493
– 3,4924Dn1 + 0,0923Dn2 = - 12,1423
2192,6773Dn2 = 26929,4252
Отсюда,
– 618,6Gсм + 2779Dn1 = - 59388,22
– 3,4924Dn1 = - 13,27574
Dn2 = 12,28
– 618,6Gсм = - 69948,42
Dn1 = 3,8
Dn2 = 12,28
Gсм = 113,08(кг / с)
Dn1 = 3,8(кг / с)
Dn2 = 12,28(кг / с)
Найдём tсм.
(Dn1 + Dn2 + Dд )ћд2 + Gокћ'ок = Gсмћсм
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.