hп1 = f(Рn1; tn1) = f(0,45МПа; 170 0C ) = 2777,4 (кДж/кг).
hп2 = f(Рn2; tn2) = f(0,2МПа; 150 0C ) = 2748,7 (кДж/кг).
hп = f(Рn; tn) = f(1,3МПа; 250 0C ) = 2927,4 (кДж/кг).
ŧд = tд · Св = 170 · 4,19 = 712,3(кДж/кг).
ŧхов = tхов · Св = 30 · 4,19 = 125,7(кДж/кг).
ŧ”ок = ts (Рn1) · Св = 147,91 · 4,19 = 619,7 (кДж/кг).
ŧ пв = ts (Рд) · Св = 164,95 · 4,19 = 691,1 (кДж/кг).
ŧд2 = ts (Рn2) · Св = 120,23 · 4,19 = 503,8 (кДж/кг).
ŧ’ок = (ts( Рn2) - Q) · Св = (120,23 - 5) · 4,19 = 482,8 (кДж/кг).
ŧок = tок · Св = 30 · 4,19 = 125,7(кДж/кг).
Подставляем найденные величины в систему уравнений:
– 11075,5 – 14008,5 – 2307,7 D n1 – 2307,7 D n2 – 2307,7 Gок = – 357808
2157,7 D n1 – 115,9 D n2 – 136,9 Gок = 0
2244,9 D n2 = 357,1 Gок
2307,7 D n1 + 2307,7 D n2 + 2307,7 Gок = 332724
2157,7 D n1 – 115,9 D n2 – 136,9 Gок = 0
2244,9 D n2 – 357,1 Gок = 0
5. Решаем данную систему уравнений методом Крамера:
Составляем матрицу:
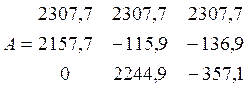
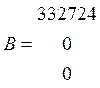
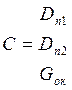
Находим главный определитель
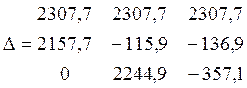 =
13760930716
=
13760930716
Находим второстепенные определители
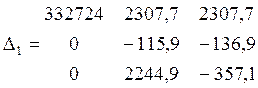 =
116025749843
=
116025749843
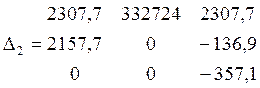 =
256368723061
=
256368723061
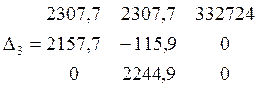 =
1611655408569
=
1611655408569
Находим искомые величины
Dn1 = Δ1/Δ = 116025749843 / 13760930716 = 8,43(кг/с)
Dn2 = Δ2/Δ = 256368723061 / 13760930716 = 18,63(кг/с)
Gок = Δ3/Δ = 1611655408569 / 13760930716 = 117,12(кг/с)
6. Решаем СЛАУ методом Гаусса:
2307,7 D n1 + 2307,7 D n2 + 2307,7 Gок = 332724
2157,7 D n1 – 115,9 D n2 – 136,9 Gок = 0
2244,9 D n2 – 357,1 Gок = 0
Умножим первое уравнение на а21 / а11 и вычтем его из второго уравнения:
2307,7 D n1 + 2307,7 D n2 + 2307,7 Gок = 332724
– 2273,6 D n2 – 2294,6 Gок = – 311097
2244,9 D n2 – 357,1 Gок = 0
Умножим второе уравнение на а32 / а22 и вычтем его из третьего уравнения:
2307,7 D n1 + 2307,7 D n2 + 2307,7 Gок = 332724
– 2273,6 D n2 – 2294,6 Gок = – 311097
2622,7 Gок = 307170
Отсюда,
Gок = 307170/2622,7 = 117,12(кг/с)
2307,7 D n1 + 2307,7 D n2 = 62446,2
– 2273,6 D n2 = – 42353,45
D n2 = – 42353,45/ –2273,6 = 18,63(кг/с)
2307,7 D n1 = 19453,75
D n1 = 19453,75/2307,7 = 8,43(кг/с)
Найдём недостающие величины
Dп = Gпв - Dд - Dхов - D n1 - D n2 - Gок
Dп = 160 – 5 – 5 – 8,43 – 18,63 – 117,12 = 5,82(кг/с)
D n1 + D n2 + Gок = G’ок
G’ок = 8,43 + 18,63 + 117,12 = 144,18(кг/с)
Заключение: при решении системы линейных алгебраических уравнений ответы получились одинаковыми.
Билет №16
Лабораторная работа №3: Методы решения систем линейных алгебраических уравнений.
Цель: ознакомится с методами численного решения систем линейных алгебраических уравнений. Получить навыки в разработке алгоритмов и программ реализующих методы решения систем линейных алгебраических уравнений. Закрепить знания по использованию пакета прикладных программ на примерах расчёта теплообменников ТЭС.
Дано: Рn1 = 0,5 МПа; tn1 = 200 0C; Рn2 = 0,18 МПа; tn2 = 180 0C; G’ок = 120 кг/с; Рок = 1,4 МПа; tок = 28 0C;
Найти: D n1; D n2; Gок; tод; t’”ок.
Составляем уравнения балансов:
D n1 + D n2 + Gок = G’ок
D n1ŧ’д2 + D n2ŧ’д2 + Gокŧ”ок = G’окŧ’”ок
D n1(hп1 - ŧд1) = Gок(ŧ”ок - ŧод)
D n1(ŧд1 - ŧ’д1) = Gок(ŧод - ŧ’ок)
D n1(ŧ’д1 - ŧ’д2) + D n2(hп2 - ŧ’д2) = Gок(ŧ’ок - ŧок)
Сложим третье и четвёртое уравнения:
D n1 + D n2 + Gок = G’ок
D n1ŧ’д2 + D n2ŧ’д2 + Gокŧ”ок = G’окŧ’”ок
D n1(hп1 - ŧ’д1) = Gок(ŧ”ок - ŧ’ок)
D n1(ŧ’д1 - ŧ’д2) + D n2(hп2 - ŧ’д2) = Gок(ŧ’ок - ŧок)
В первом уравнении выразим Gок и подставим это выражение в остальные уравнения:
D n1 (ŧ’д2 - ŧ”ок) + D n2(ŧ’д2 - ŧ”ок) = G’ок (ŧ’”ок - ŧ”ок)
D n1(hп1 - ŧ’д1) = G’ок (ŧ”ок - ŧ’ок) - D n1(ŧ”ок - ŧ’ок) - D n2(ŧ”ок - ŧ’ок)
D n1(ŧ’д1 - ŧ’д2) + D n2(hп2 - ŧ’д2) = G’ок (ŧ’ок - ŧок) - D n1(ŧ’ок - ŧок)- D n2(ŧ’ок - ŧок)
Приводим подобные
D n1 (ŧ’д2 - ŧ”ок) + D n2(ŧ’д2 - ŧ”ок) = G’ок (ŧ’”ок - ŧ”ок)
D n1(hп1 - ŧ’д1 + ŧ”ок - ŧ’ок) + D n2(ŧ”ок - ŧ’ок) = G’ок (ŧ”ок - ŧ’ок)
D n1(ŧ’д1 - ŧ’д2 + ŧ’ок - ŧок) + D n2(hп2 - ŧ’д2 + ŧ’ок - ŧок) = G’ок (ŧ’ок - ŧок)
Находим известные величины:
hп1 = f(Рn1; tn1) = f(0,5МПа; 200 0C ) = 2846,1 (кДж/кг).
hп2 = f(Рn2; tn2) = f(0,18МПа; 180 0C ) = 2819,6 (кДж/кг).
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.