Цель: ознакомится с методами численного решения систем линейных алгебраических уравнений. Получить навыки в разработке алгоритмов и программ реализующих методы решения систем линейных алгебраических уравнений. Закрепить знания по использованию пакета прикладных программ на примерах расчёта теплообменников ТЭС.
Дано: Рn1 = 0,32 МПа; tn1 = 170 0C; Рn2 = 0,15 МПа; tn2 = 150 0C; Gок = 110 кг/с; Dд = 5кг/с; tд = 140 0C; Рк = 0,007 МПа;
Найти: D n1; D n2; Dк; t’ок.
Составляем уравнения балансов:
Dn1(hn1 – ŧд1) + Dд(ŧд – ŧд1) = Gок(ŧ’”ок – ŧ”ок)
Dn2(hn2 – ŧд2) + Dn1(ŧд1 – ŧд2) + Dд(ŧд1 – ŧд2) = Gок(ŧ”ок – ŧ’ок)
Dn2 + Dn1 + Dд + Dк = Gок
Dn2ŧд2 + Dn1ŧд2 + Dдŧд2 + Dкŧк = Gокŧ’ок
Сложим второе и последнее уравнение:
Dn1(hn1 – ŧд1) + Dд(ŧд – ŧд1) = Gок(ŧ’”ок – ŧ”ок)
Dn2hn2 + Dn1ŧд1 + Dдŧд1 + Dкŧк = Gокŧ”ок
Dn2 + Dn1 + Dд + Dк = Gок
Найдём известные величины и подставим их в систему уравнений:
hп1 = f(Рn1; tn1) = f(0,32МПа; 170 0C ) = 2786,9 (кДж/кг).
hп2 = f(Рn2; tn2) = f(0,15МПа; 150 0C ) = 2753,2 (кДж/кг).
ŧд1 = ts ( Рn1) · Св = 135,75 · 4,19 = 568,8 (кДж/кг).
ŧд2 = ts ( Рn2) · Св = 111,4 · 4,19 = 466,8(кДж/кг).
ŧд = tд · Св = 140 · 4,19 = 586,6(кДж/кг).
ŧ’”ок = (ts( Рn1) - Q) · Св = (135,75 - 5) · 4,19 = 547,8 (кДж/кг).
ŧ”ок = (ts( Рn2) - Q) · Св = (111,4 - 5) · 4,19 = 445,8 (кДж/кг).
ŧк = ts ( Рк) · Св = 39 · 4,19 = 163,4(кДж/кг).
2218,1Dn1 + 89 = 11220
2753,2Dn2 + 568,8Dn1 + 2844 + 163,4Dк = 49038
Dn2 + Dn1 + 5 + Dк = 110
2218,1Dn1 = 11131
2753,2Dn2 + 568,8Dn1 + 163,4Dк = 46194
Dn2 + Dn1 + Dк = 105
Найдём Dn1, и подставим это значение в систему уравнений:
Dn1 = 11131/2218,1 = 5,02(кг/с)
2753,2Dn2 + 163,4Dк = 43338,6
Dn2 + Dк = 99,98
4. Решаем данную систему уравнений методом Крамера:
Составляем матрицу:
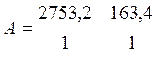
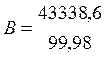
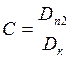
Находим главный определитель
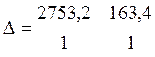 =
2589,8
=
2589,8
Находим второстепенные определители
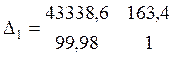 =
27001,9
=
27001,9
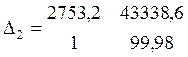 =
231926,3
=
231926,3
Находим искомые величины
Dn2 = Δ1/Δ = 27001,9/2589,8 = 10,43
Dк = Δ2/Δ = 231926,3/2589,8 = 89,55
2. Решаем СЛАУ методом Гаусса:
Dn2 + Dк = 99,98
2753,2Dn2 + 163,4Dк = 43338,6
Умножим первое уравнение на а21/а11 и вычтем его из второго уравнения
Dn2 + Dк = 99,98
- 2589,8Dк = - 231926,3
Отсюда,
Dк = - 231926,3/- 2589,8 = 89,55(кг/с)
Dn2 = 99,98 – 89,55 = 10,43(кг/с)
Найдём недостающую величину:
Dn2ŧд2 + Dn1ŧд2 + Dдŧд2 + Dкŧк = Gокŧ’ок
ŧ’ок = (Dn2ŧд2 + Dn1ŧд2 + Dдŧд2 + Dкŧк)/ Gок
ŧ’ок = (10,43 · 466,8 + 5,02 · 466,8 + 5 · 466,8 + 89,55 · 163,4)/110 = 219,8
t’ок = ŧ’ок /Св = 219,8/4,19 = 52,46 (0С)
Билет № 15
Лабораторная работа №3: Методы решения систем линейных алгебраических уравнений.
Цель: ознакомится с методами численного решения систем линейных алгебраических уравнений. Получить навыки в разработке алгоритмов и программ реализующих методы решения систем линейных алгебраических уравнений. Закрепить знания по использованию пакета прикладных программ на примерах расчёта теплообменников ТЭС.
Дано: Рn1 = 0,45 МПа; tn1 = 170 0C; Рn2 = 0,2 МПа; tn2 = 150 0C; Dд = Dхов = 5кг/с; tд = 170 0C; Рn = 1,3 МПа; tn = 250 0C; Gпв = 160 кг/с; Рд = 0,7 МПа; Рок = 1 МПа; tок = tхов = 30 0C;
Найти: D n1; D n2; Dп; Gок; G’ок.
Составляем уравнения балансов:
Dд + Dп + Dхов + G’ок = Gпв
Dдŧд + Dпhn + Dховŧхов + G’окt”ок = Gпвŧпв
D n1 + D n2 + Gок = G’ок
D n1hn1 + D n2ŧд2 + Gокŧ’ок = G’окŧ”ок
D n2(hn2 - ŧд2) = Gок(ŧ’ок - ŧок)
Сложим третье уравнение с первым, вторыми и четвёртым уравнениями
Dд + Dп + Dхов + D n1 + D n2 + Gок = Gпв
Dдŧд + Dпhn + Dховŧхов + D n1ŧ”ок + D n2ŧ”ок + Gокŧ”ок = Gпвŧпв
D n1 (hn1 - ŧ”ок) + D n2 (ŧд2 - ŧ”ок) + Gок (ŧ’ок - ŧ”ок) = 0
D n2(hn2 - ŧд2) = Gок(ŧ’ок - ŧок)
В первом уравнении выразим Dп и подставим выражение во второе уравнение.
Dп = Gпв - Dд - Dхов - D n1 - D n2 - Gок
Dд (ŧд - hn) + Dхов(ŧхов - hn) + D n1(ŧ”ок - hn) + D n2(ŧ”ок - hn) + Gок(ŧ”ок - hn) = Gпв(ŧпв - hn)
D n1 (hn1 - ŧ”ок) + D n2 (ŧд2 - ŧ”ок) + Gок (ŧ’ок - ŧ”ок) = 0
D n2(hn2 - ŧд2) = Gок(ŧ’ок - ŧок)
Находим известные величины
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.