ŧд1 = h’( Рn1) = 640,1 (кДж/кг).
ŧ’д2 = h’( Рn2) = 490,8 (кДж/кг).
ŧок = f(Рок; tок) = f(1,4МПа; 28 0C ) = 118,6 (кДж/кг).
ŧ'ок = f(Рn2; ts( Рn2) - Q) = f(0,18МПа; 116,94 - 5 0C ) = 469,6 (кДж/кг).
ŧ''ок = f(Рn1; ts( Рn1) - Q) = f(0,5МПа; 151,84 - 5 0C ) = 618,6 (кДж/кг).
ŧ’д1 = f(Рn1; t'ок + 6 … 100C) = f(0,5МПа; 111,94 + 8 0C ) = 503,7 (кДж/кг).
Подставляем найденные величины в систему уравнений:
-127,8D n1 – 127,8D n2 = 120ŧ’”ок - 74232
2491,4D n1 + 149D n2 = 17880
363,9D n1 + 2679,8D n2 = 42120
Оставим на время первое уравнение, получаем систему уравнений:
2491,4D n1 + 149D n2 = 17880
363,9D n1 + 2679,8D n2 = 42120
7. Решаем данную систему уравнений методом Крамера:
Составляем матрицу:
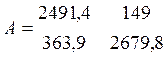
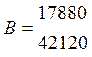
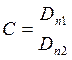
Находим главный определитель
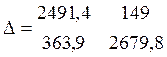 =
6622232,6
=
6622232,6
Находим второстепенные определители
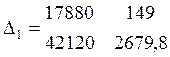 =
41638944
=
41638944
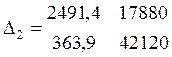 =
98431236
=
98431236
Находим искомые величины
Dn1 = Δ1/Δ = 41638944/6622232,6 = 6,29
Dп2 = Δ2/Δ = 98431236/6622232,6 = 14,86
2. Решаем СЛАУ методом Гаусса:
2491,4D n1 + 149D n2 = 17880
363,9D n1 + 2679,8D n2 = 42120
Умножим первое уравнение на а21/а11 и вычтем его из второго уравнения
2491,4D n1 + 149D n2 = 17880
2658D n2 = 39508,4
Отсюда,
Dп2 = 39508,4/2658 = 14,86(кг/с)
Dn1 = (17880 – 149 · 14,86)/2491,4 = 6,29 (кг/с)
Найдём недостающие величины:
-127,8D n1 – 127,8D n2 = 120 ŧ’”ок – 74232
ŧ’”ок = (-127,8 · 6,29 - 127,8 · 14,86 + 74232)/120 = 596,1кДж/кг
t’”ок = ŧ’”ок /Св = 596,1/4,19 = 142,3 (0С)
D n1 + D n2 + Gок = G’ок
Gок = G’ок - D n1 - D n2 = 120 – 6,29 – 14,86 = 98,85(кг/с)
D n1(hп1 - ŧд1) = Gок(ŧ”ок - ŧод)
ŧод = (D n1(hп1 - ŧд1) - Gокŧ”ок)/ Gок
ŧод = (6,29(2846,1 - 640,1) – 98,85 · 618,6)/ -98,85 = 478,2кДж/кг
tод = ŧод /Св = 478,2/4,19 = 114,1 (0С)
Билет № 17
Лабораторная работа №3: Методы решения систем линейных алгебраических уравнений.
Цель: ознакомится с методами численного решения систем линейных алгебраических уравнений. Получить навыки в разработке алгоритмов и программ реализующих методы решения систем линейных алгебраических уравнений. Закрепить знания по использованию пакета прикладных программ на примерах расчёта теплообменников ТЭС.
Дано: Рn1 = 0,45 МПа; tn1 = 180 0C; Рn2 = 0,3 МПа; tn2 = 160 0C; Рn3 = 0,15 МПа; tn3 = 140 0C; Dд = 5кг/с; tд = 150 0C; Gок = 100 кг/с; Рок = 1,2 МПа; tок = 50 0C;
Найти: D n1; D n2; Dп3; G’ок.
Составляем уравнения балансов:
Dn1 (hп1 – ŧд1) + Dд (ŧд – ŧд1) = G’ок (ŧ'''ок – ŧ''ок )
Dn1 + Dд + Dп2 + Dп3 + Gок = G’ок
Dn1ŧд1 + Dдŧд1 + Dп2hп2 + Dп3ŧд3 + Gокŧ'ок = G’ок ŧ''ок
Dn3 (hп3 – ŧд3) = Gок (ŧ'ок – ŧок )
Находим известные величины
hп1 = f(Рn1; tn1) = f(0,45МПа; 180 0C ) = 2801,9 (кДж/кг).
hп2 = f(Рn2; tn2) = f(0,3МПа; 160 0C ) = 2764,4 (кДж/кг).
hп3 = f(Рn3; tn3) = f(0,15МПа; 140 0C ) = 2729,2 (кДж/кг).
ŧд = tд · Св = 150 · 4,19 = 628,5(кДж/кг).
ŧ д1 = ts (Рn1) · Св = 147,91 · 4,19 = 619,7 (кДж/кг).
ŧ'''ок = (ts( Рn1) - Q) · Св = (147,91 - 5) · 4,19 = 598,9 (кДж/кг).
ŧ”ок = ts (Рn2) · Св = 133,54 · 4,19 = 559,5 (кДж/кг).
ŧ'ок = (ts( Рn3) - Q) · Св = (111,38 - 5) · 4,19 = 445,7 (кДж/кг).
ŧ д3 = ts (Рn3) · Св = 111,38 · 4,19 = 466,7 (кДж/кг).
ŧок = tок · Св = 50 · 4,19 = 209,5(кДж/кг).
Подставляем найденные значения в систему уравнений:
2182,2Dn1 + 44 = 39,4G’ок
Dn1 + 5 + Dп2 + Dп3 + 100 = G’ок
619,7Dn1 + 3098,5 + 2764,4Dп2 + 466,7Dп3 + 44570 = 559,5G’ок
2262,5Dn3 = 23620
Найдём Dn3 и подставим значение в систему уравнений
Dn3 = 23620/2262,5 = 10,44(кг/с)
2182,2Dn1 + 44 = 39,4G’ок
Dn1 + 5 + Dп2 + 10,44 + 100 = G’ок
619,7Dn1 + 3098,5 + 2764,4Dп2 + 4872,3 + 44570 = 559,5G’ок
39,4G’ок - 2182,2Dn1 = 44
G’ок - Dn1 - Dп2 = 115,44
559,5G’ок - 619,7Dn1 - 2764,4Dп2 = 52540,8
8. Решаем данную систему уравнений методом Крамера:
Составляем матрицу:
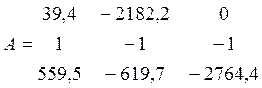
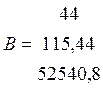
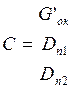
Находим главный определитель
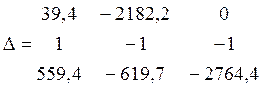 = -
4727249,8
= -
4727249,8
Находим второстепенные определители
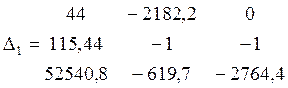 = -
581639861
= -
581639861
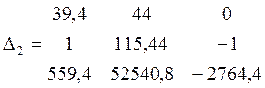 = -
10406292,5
= -
10406292,5
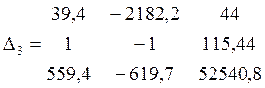 = -
25519849,3
= -
25519849,3
Находим искомые величины:
G’ок = Δ1/Δ = - 581639861/ - 4727249,8 = 123,04(кг/с)
Dn1 = Δ2/Δ = - 10406292,5/ - 4727249,8 = 2,2(кг/с)
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.