Математика \ Численные методы

Методы решения систем линейных алгебраических уравнений (Лабораторная работа № 3), страница 3

ћсм = ((Dn1 + Dn2 + Dд )ћд2 + Gокћ'ок ) / Gсм

ћсм = ((3,8 + 12,28 + 2 ) 561,5  + 95 · 540,1 ) / 113,08 = 543,52(кДж/кг).

tсм = ћсм / Св = 543,52 / 4,19 = 129,7 (0С)

Вывод: одинаковые результаты получились как при решении СЛАУ методом Крамера, так и при решении СЛАУ методом Гаусса.

Билет № 13

Лабораторная работа №3: Методы решения систем линейных алгебраических уравнений.

Цель: ознакомится с методами численного решения систем линейных алгебраических уравнений. Получить навыки в разработке алгоритмов и программ реализующих методы решения систем линейных алгебраических уравнений. Закрепить знания по использованию пакета прикладных программ на примерах расчёта теплообменников ТЭС.

Дано: Рn1 = 2 МПа; tn1 = 300 0C; Рn2 = 1,6 МПа; tn2 = 280 0C; Gпв = 120 кг/с; Рпв = 18 МПа;

tпв = 165 0C;

Найти: D n1; D n2; t”пв; tод1; tод2

 

Составляем уравнения балансов:

Dn1 (hп1 – h’п1) = Gпв (ŧ''пв – ŧсп )

Dn1 (h’п1 – ŧд1) = Gпв (ŧсп – ŧод1 )

Dn1 (ŧд1 – ŧ’д1) = Gпв (ŧод1 – ŧ’пв )

Dn2 (hп2 – ŧд2) + Dn1(ŧ’д1 – ŧд2) = Gпв (ŧ’пв – ŧод2 )

Dn2 (ŧд2 – ŧ’д2) + Dn1(ŧд2 – ŧ’д2) = Gпв (ŧод2 – ŧпв )

Сложим второе с третьим и четвёртое с последним уравнением:

Dn1 (hп1 – h’п1) = Gпв (ŧ''пв – ŧсп )

Dn1 (h’п1 – ŧ’д1) = Gпв (ŧсп – ŧ’пв )

Dn2 (hп2 – ŧ’д2) + Dn1(ŧ’д1 – ŧ’д2) = Gпв (ŧ’пв – ŧпв )

Найдём известные величины:

hп1 = f(Рn1; tn1) = f(2МПа; 300 0C ) =  3022,9 (кДж/кг).

hп2 = f(Рn2; tn2) = f(1,6МПа; 280 0C ) =  2987,9 (кДж/кг).

h'п1 = f(Рn1; ts( Рn1)  + 10 – 15 0C) = f(2МПа; 212,4 + 12 0C ) = 2826,2 (кДж/кг).

ŧпв  = f(Рпв; tпв) = f(18МПа; 165 0C ) = 707,3 (кДж/кг).

ŧ'пв = f(Рn2; ts( Рn2)  - Q) = f(1,6МПа; 201,4 - 3 0C ) = 845,1 (кДж/кг).

ŧсп = f(Рn1; ts( Рn1)  - Q) = f(2МПа; 212,4 - 3 0C ) = 895 (кДж/кг).

ŧ’д1 = f(Рn1; t'пв + 6 … 100C) = f(2МПа; 198,4 + 8 0C ) = 881,3 (кДж/кг).

ŧ’д2 = f(Рn2; tпв + 6 … 100C) = f(1,6МПа; 165 + 8 0C ) = 732,7 (кДж/кг).

Подставляем найденные величины в систему уравнений:

196,7Dn1   =  120 ŧ''пв – 107400

1944,9Dn1 = 5988

2255,2Dn2  + 148,6Dn1 = 16536                       

196,7Dn1 – 120 ŧ''пв =  – 107400

1944,9Dn1 = 5988

148,6Dn1 + 2255,2Dn2  = 16536

3.  Решаем данную систему уравнений методом Крамера:

Составляем матрицу:

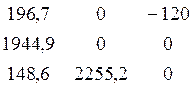
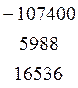А =   В =         Х =

Находим главный определитель

Δ = 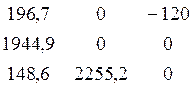   = - 526336617,6

Находим второстепенные определители

Δ1 = 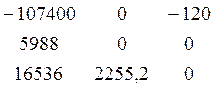   = - 1620496512

Δ2 = 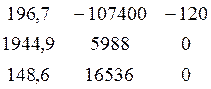   = - 3752525952

Δ3 = 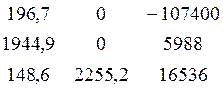   = - 473727536618

Находим искомые величины

Dп1 = Δ1/Δ = - 1620496512/-526336617,6 = 3,08 (кг/с)

Dп2 = Δ2/Δ = - 3752525952/-526336617,6 = 7,13 (кг/с)

ŧ”пв = Δ3/Δ = - 473727536618/-526336617,6 = 900 (кДж/кг)

2.      Решаем СЛАУ методом Гаусса:

196,7Dn1 – 120 ŧ''пв =  – 107400

1944,9Dn1 = 5988

148,6Dn1 + 2255,2Dn2  = 16536

Т.к. во втором уравнении коэффициенты при ŧ''пв и Dn2 равны нулю, то преобразовывать СЛАУ нет небходимости.

Dn1 = 5988/1944,9

196,7Dn1 – 120 ŧ''пв =  – 107400

148,6Dn1 + 2255,2Dn2  = 16536

Отсюда,

Dn1 = 3,08

196,7 · 3,08 – 120 ŧ''пв =  – 107400

148,6 · 3,08  + 2255,2Dn2  = 16536

Dn1 = 3,08

ŧ''пв =  (– 107400 – (196,7 · 3,08))/ – 120

Dn2  = (16536 – (148,6 · 3,08))/2255,2

Dn1 = 3,08

ŧ''пв =  900

Dn2  = 7,13

Найдём t”пв

t”пв = ŧ”пв /Св = 900/4,19 = 214,8 (0С)

Найдём остальные недостающие искомые величины

Dn1 (h’п1 – ŧд1) = Gпв (ŧсп – ŧод1 )

ŧод1 = (Gпвŧсп – Dn1 (h’п1 – ŧд1))/ Gпв

ŧд1 = h’( Рn1) = 908,4 (кДж/кг).

ŧод1 = (120 · 895 – 3,08 (2826,2 – 908,4))/ 120 = 845,8

tод1 = ŧод1/Св = 845,8/4,19 = 201,9 (0С)

Dn2 (ŧд2 – ŧ’д2) + Dn1(ŧд2 – ŧ’д2) = Gпв (ŧод2 – ŧпв )

ŧод2 = (Dn2 (ŧд2 – ŧ’д2) + Dn1(ŧд2 – ŧ’д2) + Gпвŧпв)/ Gпв

ŧд2 = h’( Рn2) = 858,4 (кДж/кг).

ŧод2 = (7,13 (858,4 – 732,7) + 3,08(858,4 – 732,7) + 120 · 707,3)/ 120 = 718

tод2 = ŧод2/Св = 718/4,19 = 171,4 (0С)

Заключение: при решении СЛАУ методами Крамера и Гаусса искомые величины получились одинаковыми.

Билет № 14

Лабораторная работа №3: Методы решения систем линейных алгебраических уравнений.

Скачать файл