В. Л. ДРОЗД, М. А. УРБАН. От маленьких проблем - к большим открытиям // НАЧАЛЬНАЯ ШКОЛА, 2000. - №5- с.37-39.
Проблемной ситуацией в обучении не обязательно должна быть задача, вызывающая у школьников серьезные затруднения. Более того, большие, сложные проблемы, выдвигаемые порой на уроках, вместо стимулирования интеллектуальной деятельности ребенка по поиску решения могут вызвать обратную реакцию: блокировать мыслительную активность. Причина -- неверие ребенка в собственные силы, страх перед потенциальной неудачей, вызванные «глобальностью» поставленной проблемы.
Более продуктивными и гуманными в процессе обучения младших школьников, с нашей точки зрения, являются небольшие проблемные задания. Получив опыт работы над такими заданиями, испытав своеобразное интеллектуальное «удовольствие» при нахождении искомого, учащиеся естественным образом будут пытаться применить освоенные процедуры в средней и старшей школе.
Одним из возможных путей создания проблемных ситуаций «малого масштаба» может быть организация на уроках математики исследований, в которых реализуются не только знания, но и методы их получения.
В качестве примера покажем, как небольшое по объему и сложности исследование проблемной ситуации может помочь учащимся глубже осознать некоторые математические закономерности.
В теме «Письменное деление на двузначное число» дети учатся делить на круглые числа с остатком. В нашем опыте при изучении этого материала на уроках несколько раз возникала проблемная ситуация: учащиеся начинали сомневаться в истинности правила деления числа на произведение.
Следуя учебнику (Математика-4 / Под ред. А. А. Столяра. - Народная асвета, 1995), учащиеся выполняют деление 168 : 40 устно следующим образом: 168 : 40 = 168 : (40 • 10) = 168 : 10 : 4 = 4 (ост. 8). При этом, выполняя последовательно деление 168 : 10 : 4, не обращают внимание на промежуточные остатки при делении, а итоговый остаток (8) определяют, умножив результат (4) на делитель (40) и вычтя полученное значение (160) из делимого (168).
Аналогично рассматривается данный прием на примере деления 638 на 90 в учебнике М. И. Моро и др. для III класса трехлетней и IV класса четырехлетней начальной школы.
На анализируемом уроке учитель предпочел записать последовательно каждый этап процесса деления. Решение примера 168 : 40 оформил следующим образом:
168 : 10= 16 (ост. 8) 16 : 4 = 4
Учащиеся, уже знакомые с правилом деления числа на произведение, поинтересовались, можно ли делить в другом порядке - сначала на 4, а потом на 10. Предположение тут же было проверено и получен непредвиденный результат:
168 : 4 = 42 42 : 10 = 4 (ост. 2)
При разборе следующего примера 376 : 30 проблемная ситуация не разрешилась. Находя ответ по схеме, предложенной в учебнике, т.е. выполнив деление, не акцентируя внимания на промежуточных остатках, учащиеся получили ответ 12, а затем умножили его на делитель 30 и получили 360. Это означает, что 376 - 360 = 16 единиц остались не разделенными. Таким образом, был найден ответ - 12 (ост. 16).
После этого дети вместе с учителем оформили запись решения по-другому:
376 : 30 = 376 : (3 • 10)
|
1-й способ 376 : 10 = 37 (ост. 6) 37 : 3 = 12 (ост. 1) |
2-й способ 376 : 3 = 125 (ост. 1) 125 : 10 = 12 (ост. 5) |
Получив результаты, все с удивлением обнаружили, что ни один из них не соответствует первоначально найденному значению 12 (ост. 16). Создалась ситуация, «провоцирующая» ученика усомниться в истинности изученного теоретического правила.
Средствами математического аппарата эта проблемная ситуация разрешается следующим образом. Из того, что каждое целое неотрицательное число можно представить в виде
а = bq + r ( r < b) следует согласно способу 1, что:
376 = 37 • 10 + 6 37= 12 • 3+ 1
![]() 376 = (12 •
3+1) • 10 + 6= 12 • (3 • 10) + 1 • 10 + 6 = 360+16
376 = (12 •
3+1) • 10 + 6= 12 • (3 • 10) + 1 • 10 + 6 = 360+16
r
В то же время согласно способу 2:
376= 125•3+1 125= 12•10 + 5
![]() 376 =
(12•10 + 5)•3 + 1 = 12•(10•3) + 5 • 3 + 1 = 360+16
376 =
(12•10 + 5)•3 + 1 = 12•(10•3) + 5 • 3 + 1 = 360+16
r
Таким образом, остаток 16 в одном и другом случае представлен различными числовыми выражениями (1 • 10 + 6 и 5 • 3 + 1). Усмотрев математическую суть данной проблемы (остатки, полученные на первом и втором этапах деления, имеют различное значение), учителю легче подобрать адекватные средства исследования проблемной ситуации младшими школьниками.
Одним из таких средств может выступить наглядность, отражающая существенные стороны процесса деления - модель (чертеж, иллюстрация и т.п.). Вначале учащимся предлагается показать на отрезке деление по содержанию на 10. Предлагается разбить большой отрезок на отрезки длиной по 10 клеток. В результате получится 37 отрезков длиной по 10 клеток каждый и 6 клеток, которые не образуют группу в 10 клеток, - это остаток первого шага деления (рис. I).
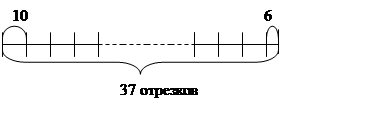 376: 10 =
37 (ост. 6)
376: 10 =
37 (ост. 6)
Рис. 1
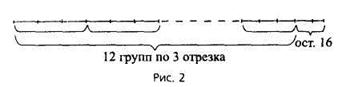
После этого предлагается самостоятельно показать на чертеже второй шаг деления. Выполняя это задание, многие учащиеся замечают, что делимое 37 на втором этапе деления обозначает не 37 единиц, а 37 десятков. Сгруппировав эти десятки по 3, замечают, что образовалось 12 групп по 3 десятка в каждой. При этом последний десяток не вошел ни в одну группу, т.е. остался не разделенным. Дети замечают, что остаток 1 на втором этапе деления имеет совершенно иное значение - он обозначает 1 неразделенный десяток. В итоге имеем остаток, состоящий из одного десятка и шести единиц, т.е. 16 (рис. 2).
37 : 3 = 12 (ост. I)
10 10 6
Выполняя деление в другом порядке, учащиеся вначале иллюстрируют на чертеже деление по содержанию 376 на 3. В результате получается 125 «троек» и 1 единица остается не разделенной (рис. 3).
376 : 3 = 125 (ост. 1)
3 1
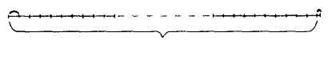
125 отрезков
Рис.3.
Выполняя второй шаг деления, учащиеся замечают, что делимое 125 обозначает 125 «троек». В результате деления на 10 получается 12 групп по 10 «троек» в каждой группе. При этом последние пять «троек» не образуют группу в 10 «троек», т.е. остаются не разделенными. Таким образом, остаток 5 на втором этапе деления обозначает количество неразделенных «троек», а не единиц. В итоге имеем остаток, состоящий из пяти «троек» и одной единицы, т.е. 16 (рис. 4).
125 : 10= 12 (ост. 5)
333331
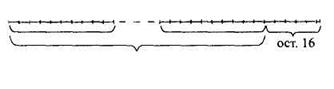
12 групп по 10 отрезков
Рис. 4
Теперь легко объяснить результаты, полученные в первом примере. При делении 168 на 4 получаем 42 «четверки», которые при делении на 10 дают частное 4 и в остатке 2 «четверки», т.е. 8 единиц.
Таким образом, для проведения исследования, направленного на разрешение данной проблемной ситуации, оказались необходимыми как математическая подготовка учителя (для уяснения математической сути проблемы), так и его методическая квалификация (для организации поиска решения проблемы младшими школьниками средствами учебного моделирования).
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.