Извлечение и ускорение пучков положительных ионов, страница 6

Поскольку величина р_х постоянна по всему поперечному сечению пучка, обычно используются графики эмиттанса, в которых по ординате откладывается только величина а. В этом случае при ускорении пучка будет меняться и площадь, охваченная огибающей.

Из утверждения о сохранении    поперечного эмиттанса   (не вполне справедливого, как отмечается ниже)  следует, что пу-

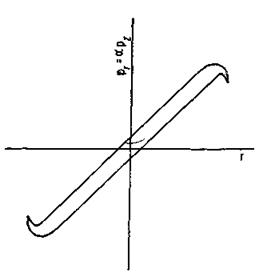
Рис. 5.11. Возможная диаграмма эмиттанса для пучка, обладающего цилиндрической симметрией

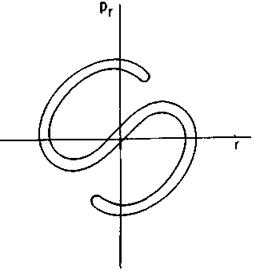
Рис. 5 12 Диаграмма эмиттанса ионного пучка с "воздушными полостями"

чок с наклонной диаграммой эмиттанса (рис. 5.11) можно трансформировать в пучок малого диаметра с большой угловой расходимостью, диаграмма эмиттанса которого имеет вид длинного узкого вертикального эллипса вблизи г = 0, или в параллельный пучок большого диаметра, изображаемый горизонтальным эллипсом, охватывающим точки вблизи а = 0. Даже если змиттанс можно считать постоянным, плохая оптика может сформировать пучок, имеющий диаграмму эмиттанса сложной формы (рис. 5.12). Говорят, что такая диаграмма имеет «воздушные полости», ее трудно трансформировать в компактную площадь в координатах . При плохой ионной оптике эффективный эмиттанс пучка будет больше действительного.

Преобразование инвариантного шестимерного объема фазового пространства в инвариантный двумерный эмиттанс в предположении постоянства V_z может быть применено, но не является строгим. Существует возможность уменьшить поперечный эмиттанс за счет увеличения разброса по z-компоненте скорости. В работе [275], например, описана система ускорения,   в которой расчетные огибающие траектории сближались в 10 раз, в то время как разброс поперечных компонент скорости увеличился только в 3 раза, что соответствует уменьшению эмиттанса в ~3 раза. Луч света характеризуется инвариантной величиной плотности мощности, приходящейся на единицу телесного угла. Соответствующая величина для ионного пучка называется яр костью и равна

                                                                     (5.15)

где J — плотность тока и Ω — разброс по телесному углу в каждой точке. Разброс по телесному углу пропорционален α2, где α — угловое распределение в каждой точке; площадь пропорциональна r², поэтому с точностью до постоянных коэффициентов выражение (5.15) приводится к виду

                                                                (5.16)

Поскольку приближенное выражение для эмиттанса выглядит как

                                                                (5.17)

a  пропорционально ускоряющему напряжению V, то можно написать

                                                                (5.18)

Ленгмюр показал [166], что плотность тока частиц (напри мер электронов, испускаемых термоэмиттером) с максвелловским распределением по скоростям, достижимая в произвольной точке, ограничена величиной

                                     (5.19)

которая обычно может быть приближенно записана в виде

                                                      (5.20)

Максимально возможная яркость при этом равна

                                                           (5.21)

Хотя ионы эмитируются не с максвелловским распределением скоростей (рис. 3.10), однако, если в уравнение (5.21) подставить электронную температуру плазмы источника, то можно получить верхний предел достижимой величины яркости.

Более подробное описание эмиттанса и яркости, а также других параметров, которыми характеризуется ионный пучок, можно найти в работах [244, 87, 88]

5.5. Многоапертурные ускоряюще-замедляющие системы извлечения

Согласно ходу рассуждений в разд. 5.1 и полученному ра венству (5.4), первеанс одиночного отверстия ограничен вели чиной  или  в случае длинной щели. Это ограничение эквивалентно ограничению максимального норми рованного первеанса величиной П=1, как указано в задачах 5.3—5.5. Чтобы получить токи большей величины, необходимо использовать большее количество отверстий или щелей (см. рис. 1.1). Как следует из решения задачи 5.6, в сильноточных ионных источниках число круглых апертур может составлять величину  порядка  нескольких сотен или даже тысяч.