Извлечение и ускорение пучков положительных ионов, страница 4

Б. Нерасходящиеся цилиндрические пучки

Тот же подход можно использовать применительно к пучкам с круглым поперечным сечением. В этом случае необходимо определить форму электродов, которые создадут вне пучка поле, соответствующее заданному равенством (5.9) значению потенциала на границе пучка, и нулевое поперечное поле на границе.   В этом случае вместо dV/dy = 0 следует писать dV/dr = 0.

Простой аналитический метод, хорошо проявивший себя в случае пучка с плоской границей, в этом случае не подходит. Необходимо найти другие возможности. Пирс [229] описал метод электролитической ванны¹⁾ для определения требуемой формы электродов (рис. 5.6). В основе ускоряющей системы (рис. 5.7) лежит именно эта геометрия электродов (рис. 5.6). Фокусная длина для  круглой  апертуры   [230]   равна

                                                                     (5.14)

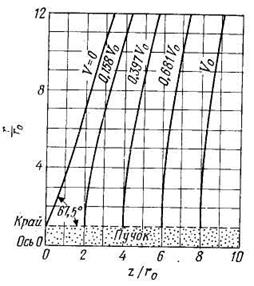
Рис. 5.6. Эквипотенциальные поверхности, соответствующие цилиндрическому пучку, ограниченному объемным зарядом.

Для  и  получим . Ионы, подходящие к последней апертуре, двигаясь параллельно оси, расходятся (рис. 5.7).

Когда электроды простираются достаточно далеко от пучка ,(рис. 5.5 и рис. 5.7), то поля в пучке полностью определяются геометрией электродов. Если боковые размеры системы строго ограничены и электроды не могут быть продолжены далеко от пучка, для получения требуемого поля следует использовать дополнительные электроды, расположив их по эквипотенциальным поверхностям между первым и последним электродами (рис. 5.8).

В. Сходящиеся пучки

Электродные системы (рис. 5.5 и рис. 5.7) формируют пучки электронов или ионов, движущихся по параллельным траекториям между эмиттером и ускоряющим электродом. Предпочтительно создавать в этой области сходящийся пучок (рис. 5.1, в). Поскольку есть выражение для распределения потенциала в случае цилиндрического сходящегося пучка [уравнение  (2.25)]     с коэффициентом β²,  приведенным  в табл. 2.1  в

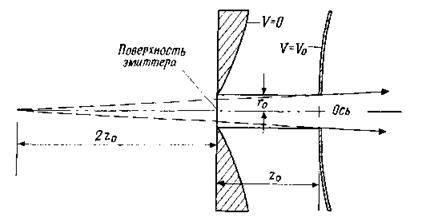
Рис. 5.7. Электроды системы извлечения цилиндрического ионного пучка; расходимость пучка обусловлена дефокусирующим действием выходной апертуры.

Рис. 5.8. Электроды системы формирования пучка в условиях ограниченного бокового пространства.

виде (-β²), и для случая сферического сходящегося пучка (2.26) с коэффициентом α², приведенным в той же таблице в виде (α²), можно приманить разработанный метод.

Например, в работе [229] приведено решение для пучка, получаемого с цилиндрического эмиттера и сжимающегося до четверти начальной ширины.

Эквипотенциальные поверхности поля, формирующего сходящийся пучок, представляют собой концентрические цилиндры, за исключением области вблизи выходной апертуры, где встречаются поля рассеяния, и поверхности нулевого потенциала, составляющую, как обычно, угол 67,5^oC поверхностью пучка (рис. 5.9). В реальном ускорителе электроды, представляющие эти поверхности, должны быть размещены по обеим сторонам сходящегося пучка.

Случай сходимости в точку вдоль радиусов сферы является более сложным, так как существуют два характеристических радиуса: радиус сферы r₀ (рис. 5.10) и радиус эмиттера а/2, т. е. радиус r₀ и угол θ, образованный траекториями самых крайних сходящихся ионов и осью. Форма электродов (рис. 5.10) не рассчитывалась, и мы не будем пытаться найти пирсовскую геометрию для случая сферически симметричной сходимости. Каким образом можно ее определить для некоторых заданных значений r₀ и θ и выбранной степени сжатия пучка в электродной системе? Во-первых, из уравнения  (2.23)  необ-

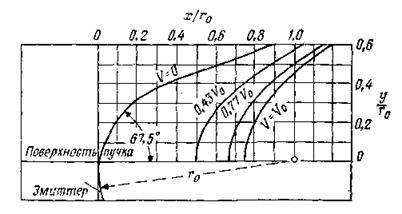
Рис. 5.9. Форма эквипотенциален, необходимая для создания сходимости пучка к оси в случае, когда ширина выходной щели составляет четвертую часть ширины эмиттера.

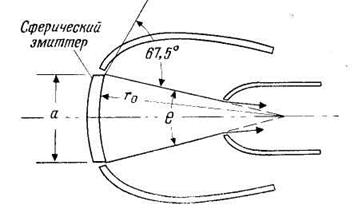
Рис. 5.10. Схематическое изображение электродов Пирса для сходящегося пучка в случае сферической симметрии.

ходимо найти ток I, для фиксированного значения I определить V(r) и потом получить решение уравнения Лапласа вне пучка, удовлетворяющее граничным условиям V=V(r) и dV/dθ = 0 на краю пучка.