Извлечение и ускорение пучков положительных ионов, страница 2

                                            (2.116)

Можно сказать, что одиночная апертура или щель имеет максимальный нормированный первеанс порядка 1; мы можем предполагать, что ускоряющие электроды, разработанные для создания пучков с малой угловой расходимостью, должны обладать малым по сравнению с 1  нормированным первеансом.

Малому угловому расхождению ионов пучка обычно соответствуют величины нормированного первеанса порядка 0,15. Иногда первеанс сопоставляют с теоретической величиной Ро, базирующейся на модели параллельного потока с плотностью тока, равной

где V — напряжение между  электродами, расположенными на расстоянии L друг от друга. Соответственно ток с эмиттера площадью S равен

что дает для теоретической величины первеанса значение

Отношение действительного значения первеанса к Ро можно записать как

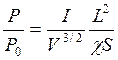                                                            (5.5)

Это отношение служит мерой эффективности электродной системы при данной геометрии по отношению к идеальной системе в отличие от нормированного первеанса, который определяет эффективность электродной системы! в сравнении с не зависящей от межэлектродного расстояния максимально возможной эффективностью. Отношение этих двух параметров можно выразить следующим образом:

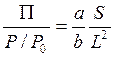                                                            (5.6)

что сводится к значению (πr²/L²)  для круглого и  (a/L)² для щелевого эмиттера шириной а.

5.3. Пирсовские электроды

Несмотря на то что ионы на границе плазмы обладают энергией направленного движения, называемой энергией Бома, равной kT/2 и составляющей в плазме ионного источника величину порядка 3 эВ, влияние этого движения будет мало, если ионы ускоряются до энергии в несколько килоэлектрон-вольт и выше. В первом приближении будем считать, что ионы' стартуют с границы плазмы без начальной скорости. Кроме того, пренебрежем существующим на границе плазмы (т. е. в области плазма — слой) полем очень малой величины. В первую очередь определим конструкцию электродов, позволяющих получить параллельный пучок из длинной щели. Использованный здесь подход будет полезен при разработке электродов для прямолинейного потока вообще, включая цилиндрические или сферические сходящиеся пучки.

А. Ленточные пучки без расходимости

Вспомним задачу о токе, ограниченном объемным зарядом, между бесконечными плоскопараллельными электродами (см. разд. 2.2). Частицы, выходящие с нулевой скоростью с поверхности, на которой (dV/dx) =0, движутся по силовым линиям к коллекторной плоскости. Изменение потенциала, описываемое уравнением   (2.7),  может  быть  записано  в  виде

где  Как и выше (см. разд. 2.2), будем решать задачу для электронов, полагая, что V везде неотрицательно и равно 0 на эмиттере. Использование результатов применительно к ионам не вызовет затруднений.

Метод  Пирса   [229, 230]   заключается     в удалении    части пучка, находящейся в области по одну сторону от плоскости, параллельной направлению распространения  пучка,  например y=0 (рис. 5.3), и замене ее электродами,  которые  воспроизводили   бы  граничные условия на этой плоскости таким образом, что частицы, движущиеся в области   у<0,   являлись   как бы частью всего  потока   между бесконечными параллельными плоскостями. Таким образом, задача  с объемным зарядом   была   сведена   к   нахождению решения  V(x, у)  двумерного    уравнения Лапласа

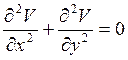
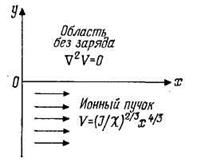
Рис. 5.3. Необходимые условия для формирования  параллельного пучка.

удовлетворяющего граничным условиям

dV/dy = 0    при    y = 0                                                                             (5.7)

                                                                                         (5.8)

где для частиц, стартующих с границы с нулевым полем из состояния покоя, равно

                                                                           (5.9)

Решением этой краевой задачи является действительная часть функции