Извлечение и ускорение пучков положительных ионов, страница 3

                                                                               (5.10)

где i—мнимая единица . Очевидно, решение (5.10) удовлетворяет уравнению (5.8). Более того, (x+iy)^4/3  является аналитической функцией). У этих функций и действительная, и мнимая части удовлетворяют уравнению Лапласа, так что это требование выполняется. Наконец, поскольку замена в (5.10) i на -i не влияет на V, ясно, что замена у на -у ничего не изменяет. Для четной по у аналитической функции V производная dV/dy = 0 при у =0. Поэтому распределение потенциала, которое должно быть создано в области y>0 (рис. 5.3), равно

                                                    (5.11)

Уравнение (5.11) может быть записано в виде

Соответствующая V=0 эквипотенциальная кривая образует с осью х угол, определяемый из условия 4/3 arctg(у/х)  = π/2 и равный Зπ/8 рад, или 67,5° (рис. 5.4).

Разделив   V на  значение  потенциала , равное

получим нормированный потенциал

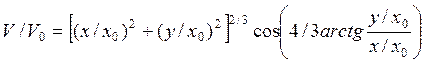                           (5.12)

Все эквипотенциали, соответствующие положительным значениям нормированного потенциала, за исключением эквипотенциали, соответствующей Vo, в относительных координатах имеют один и тот же вид (рис. 5.4). Все положительные эквипотенциали (положительные для электронов, отрицательные для ионов)  у края пучка перпендикулярны    направлению его распространения и до расстояния х₀ от края хорошо описываются  цилиндрами радиуса 3х₀ (рис. 5.4). Располагая электроды с потенциалами 0 и Vo по указанным поверхностям, мы обеспечим такие граничные условия, при которых заряженные частицы будут двигаться прямолинейно, даже находясь на краю  пучка.

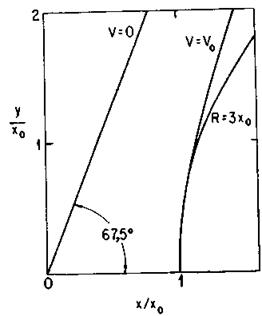
Рис.    5.4.     Эквипотенциальные     по-   верхности,     соответствующие  парал-  лельному   пучку  ионов,  ограниченному нескомпенсированным   объемным   зарядом.

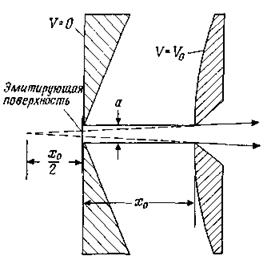
Рис. 5.5. Электроды    системы извлечения   ленточного   пучка;      расходимость  пучка    обусловлена дефокусирующим   действием   выходной   апертуры.

Для формирования ленточного пучка необходимо поместить электроды, имеющие щелевую апертуру с обеих сторон пучка (рис. 5.5). Выходная щель действует на пучок подобно дефокусирующей линзе, что ведет к некоторой его расходимости. Фокусное расстояние длинной щели [230] равно

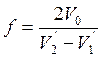                                                                              (5.13)

где V2 и V1 — градиенты потенциала на выходной и входной сторонах щели соответственно.

В случае, который имеет место для пучка с некомпенсированным объемным зарядом,  и если принять , получим f = -1,5 x_о, что приводит к расхождению пучка

(рис. 5.5). Данный эффект можно устранить, если поместить в апертуру электрода, находящегося под потенциалом Vo, тонкую сетку, однако в интенсивных ионных пучках этому препятствуют нагрев и распыление материалов сетки.

Используя указанный метод, мы сначала приняли, что эквипотенциальные поверхности вне пучка представляют собой па раллельные плоскости, а затем модифицировали результат с помощью уравнения (5.13). Для того чтобы погрешность результатов, полученных при использовании этого метода, была невелика, требуется, чтобы расстояние х₀ было намного боль ше ширины щели а. Как минимум отношение х_о/а должно быть не менее 4. Влияние выходной апертуры, названное задачей об анодном отверстии, изучалось подробно [155], однако приведенное здесь приближенное выражение является достаточно точным для большинства приложений.

Эмитирующая  поверхность заслуживает особого внимания. Если  она  представляет    собой     поверхность    твердотельного электронного эмиттера или обсуждаемый в гл. 9 поверхностно-ионизационный  эмиттер     ионов,  то для  выполнения  условий, при  которых  справедлив наш  подход   (рис.5.5), помимо требования eV₀ >> начальная  энергия  ионов,  источник  должен  по меньшей мере обеспечивать плотность тока, равную плотности в режиме ограничения эмиссии объемным зарядом. Если эмитирующей  поверхностью служит  граница   плазмы,  то  зависимость   между  номинальной   плотностью   тока   и  напряжением для данного х0 должна описываться уравнением Чайлда. Если плазма  создает плотность тока,  большую,    чем номинальная, ее эмитирующая  поверхность будет выгибаться наружу   (рис. 5.1,б)   и ионный  пучок  будет расходиться в межэлектродном пространстве.