Извлечение и ускорение пучков положительных ионов, страница 11

Экспериментальная программа такого плана была выполнена авторами работы [54] для трехэлектродной системы (рис. 5.17). Было обнаружено, что наиболее критичным параметром является отношение радиуса апертуры r₁ к расстоянию между плазменным и ускоряющим электродами d₁. Были получены максимальная для данного напряжения плотность тока и минимальная угловая расходимость для отношения r₁/d₁>0,5, т. е. в случае, когда диаметр отверстия больше расстояния между первыми двумя электродами. Параметры пучка чувствительны к величине отношения r₂/r₁, однако необходимо сделать это отношение больше 0,75, чтобы избежать попадания лучка на ускоряющий электрод. Оказалось, что изменение радиуса выходной апертуры r₃ не оказывает влияния на пучок. Было установлено [54], что необходимо делать замедляющий промежуток d₂ по возможности минимальным. Это, вероятно, объясняется фокусирующим действием, обсуждавшимся выше (см. разд. 5.4, а также рис. 5.15,6). Было также обнаружено, что толщина D₁ плазменного электрода оказывает определенное влияние и оптимальным является .

Кроме того, исследовалось влияние отрицательного (замедляющего) напряжения V^-. Оказалось, что это напряжение должно быть больше, чем 0,03 V⁺, чтобы избежать обратного потока электронов. В данной геометрии системы увеличение V⁺ свыше указанной величины оказывает очень слабое влияние на ток, идущий на приемник малого углового размера.

Другой подход к конструированию электродов [142] предполагает моделирование с использованием электролитических ванн. Однако этот метод может быть заменен вычислительными методами, так что нет необходимости обсуждать его здесь. В численных методах при одном из подходов выбирают геометрию электродов и распределение потенциалов. Затем должно быть сделано предположение о формах границ плазмы источника и пучка. Вначале необходимо найти решение V(х,у,z) уравнения Лапласа при этих границах. Следующий шаг - вычисление траекторий ионов, стартующих из состояния покоя с предполагаемой границы плазмы источника. Затем, вводя плотность тока с границы, получают плотность объемного заряда р во всех точках. Новую функцию V(х, у, z) находят из уравнения Пуассона при подстановке в него функции р(х, у, z). Затем необходимо вновь рассчитать траектории и произвести итерации до получения самосогласованного набора траекторий и потенциалов. Плотность тока на границе плазмы должна быть затем исправлена таким образом, чтобы окончательное решение соответствовало очень близкому к нулю значению градиента потенциала на всех границах плазмы. Мерой того, будут ли предполагаемые границы плазмы действительными, является однородность плотности тока на всей границе плазмы, а мерой приемлемости формы электродов    и формы границы

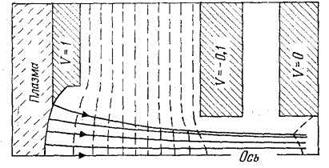
Рис. 5.18. Геометрия электродной системы с круглой апертурой Купера, Беркнера и Пайла (показаны рассчитанные траектории ионов и экви-потенциали).

плазмы является характер поведения пучка при прохождении им последнего электрода.

Подобные исследования, проведенные авторами работы [51], позволили в результате последовательных приближений получить для круглой апертуры (рис. 5.18) и для щели (рис. 5.1.9) ряд траекторий, параллельных в пределах ±1°. Результаты измерения рабочих характеристик этих источников очень хорошо повторили расчетные характеристики. Пучок имел га-

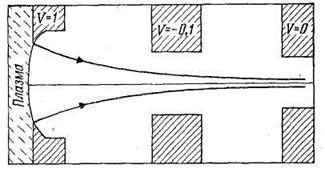
Рис. 5.19. Геометрия электродной системы с длинной щелью Купера, Беркнера и Пайла (показаны потенциалы электродов и граничные траектории ионного пучка).

уссов профиль с шириной по уровню 1/е, равной ±1,23° при одноапертурном коллекторе и ±1,31° при 40%-ной прозрачности эмиссионного электрода. Вычисленный первеанс был равен  для   и для , а измеренный первеанс при использовании    19-апертурного экстрактора находился в диапазоне между вычисленными значениями  и . В этих экспериментах не исследовалась выходная структура пучка, но результаты следует оценивать как подтверждение работоспособности компьютерной программы. Измеренное значение первеанса 6,5-10~9 А/В3/2 для 0+ соответствует нормированному первеансу 0,17, что составляет 0,49 значения Ро, вычисленного на основании величины тока между поверхностью плазмы и электродом, полученной из уравнения Чайлда, где за величину ускоряющего промежутка принимается расстояние от плазмы до передней части ускоряющего электрода.