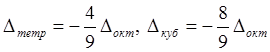Энергетические уровни примесных ионов в кристаллах, страница 5

.                            (3)

В подавляющем большинстве неорганических соединений октаэдр, тетраэдр и куб отражают лишь координацию центрального иона, но не локальную симметрию поля в этой позиции. Искажение координационных полиэдров приводит к дополнительному расщеплению уровней. Кроме того, если октаэдрическое координационное окружение примесного иона искажается так, что две валентные связи, вытянутые вдоль какой-нибудь одной оси, становятся короче или длиннее остальных четырех, то e_g-орбиталь дополнительно расщепляется на два подуровня, из которых верхний соответствует -орбитали, а t_2g-орбиталь также расщепляется на два подуровня, верхний из которых соответствует d_xy–орбитали свободного иона. Это расщепление называется статическим эффектом Яна-Теллера. Он наиболее характерен для 3d⁹, 3d⁷ и 3d⁴ ионов.

В общем случае задача построения диаграмм энергетических уровней 3d-ионов в кристаллическом поле решается с учетом влияния поля лигандов, электростатического и спин-орбитального взаимодействий оптических d-электронов. Такие диаграммы для всех 3d^N –электронных конфигураций впервые были построены Й. Танабе и С. Сугано. Поэтому они называются диаграммами Танабе-Сугано. Диаграммы (рис. 10а) показывают зависимость параметра Рака В, характеризующего межэлектронное взаимодействие и энергию уровня, от величины кристаллического поля.

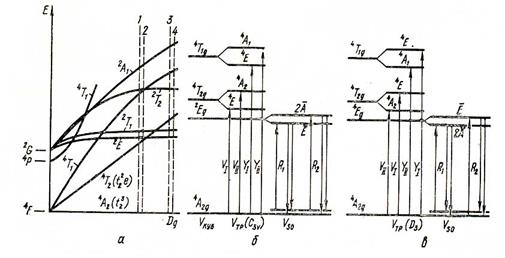
Рис.10. Диаграмма Танабе-Сугано для примесного иона Cr³⁺ (а) и положение его энергетических уровней в рубине (б) и изумруде (в).

Если величина кристаллического поля известна (известен кристалл), то из диаграммы Танабе-Сугано можно построить диаграммы уровней примесного иона в этом кристалле, подобные диаграммам Гротриана для свободных атомов и ионов. Для этого на диаграммах Тунабе-Сугано из точке на оси абсцисс, соответствующей известной величине 10Dq, проводится параллельная оси ординат линия, и по точкам ее пересечения с кривыми расщепления строится диаграмма Гротриана.

Для обозначения энергетических уровней примесного иона используется символика групп симметрии: ^2S+1Г_n – похожая на символику LS-связи. Как показал Безе, для октаэдрической симметрии возможны всего пять типов состояния поля лигандов, которые он обозначил через квантовые числа Г_n, где n=1,2,3,4,5. Другие авторы используют иную символику. Поскольку эти обозначения пока не унифицированы, то в ниже расположенной таблице приведены соответствия наиболее распространенных обозначений

При помещении иона в кристалл с октаэдрической симметрией поля уровни свободного иона преобразуются в следующие состояния

В электронных переходах существенную роль играют правила отбора, которые определяют интенсивность спектральных полос. Напомню, что в случае свободного иона для всех видов связи запрещены переходы без изменения четности уровней, т.е. запрещены переходы типа d«d и f«f. Этот запрет частично снимается для ионов, помещенных в поле лигандов, под влиянием их ассиметричного расположения или нечетных колебаний самих примесных ионов. При этом силы осцилляторов на таких переходах имеют порядок f=10^-4 –10^-5. Кроме того, в примесном ионе часто такие переходы оказываются разрешенными как магнито-дипольные (f=10^-6) или электро-квадрупольные (f=10^-7). Запрет по изменению спина, действующий в приближении LS-связи для свободных ионов, для примесных ионов частично снимается за счет спин-орбитального взаимодействия, смешивающего волновые функции термов с разной мультиплетностью за счет колебаний ионов. В этом случае сила осциллятора таких интеркомбинационных переходов достигает значения f=10^-6– 10^-7. Кроме того, для таких переходов отличны от нуля магнито-дипольные и электро-квадрупольные моменты, которые обеспечивают значение силы осцилляторов на уровне f=10^-9 – 10^-10.