Лекция 3.
ИЗЛУЧЕНИЕ И ПОГЛОЩЕНИЕ СПЕКТРАЛЬНЫХ ЛИНИЙ. ИНТЕНСИВНОСТЬ И ШИРИНА СПЕКТРАЛЬНОЙ ЛИНИИ.
Излучение. В соответствии с законами классической электродинамики каждая ускоренно движущаяся заряженная частица, в том числе и электрон, излучает электромагнитные волны. В частности, колеблющийся или вращающийся электрон, который называется осциллятором, излучает среднюю по времени мощность
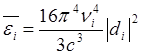 (1)
(1)
на монохроматической волне с
циклической частотой 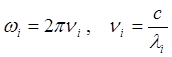 . Здесь ni
– обычная частота электромагнитной волны, измеряемая, как и циклическая частота
в герцах, li - длина этой волны, которая в оптическом
диапазоне измеряется в микрометрах и нанометрах, c
– скорость света, di = eai - дипольный момент частицы, e –элементарный заряд, ai
– амплитуда его колебания на частоте wi. Пусть в единице объеме находится
. Здесь ni
– обычная частота электромагнитной волны, измеряемая, как и циклическая частота
в герцах, li - длина этой волны, которая в оптическом
диапазоне измеряется в микрометрах и нанометрах, c
– скорость света, di = eai - дипольный момент частицы, e –элементарный заряд, ai
– амплитуда его колебания на частоте wi. Пусть в единице объеме находится 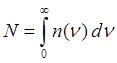 осцилляторов, способных излучать
электромагнитные волны во всем диапазоне частот. Из них на монохроматической
волне с центром при ni в интервале частот
осцилляторов, способных излучать
электромагнитные волны во всем диапазоне частот. Из них на монохроматической
волне с центром при ni в интервале частот ![]() ,
излучают только
,
излучают только ![]() осцилляторов, где n(n) –
распределение осцилляторов по частотам излучения. В этом случае мощность
излучения на монохроматической волне с единицы объема вещества равна
осцилляторов, где n(n) –
распределение осцилляторов по частотам излучения. В этом случае мощность
излучения на монохроматической волне с единицы объема вещества равна
![]() ,
(2)
,
(2)
здесь используется величина fni £1 , которая называется сила осциллятора в излучении.
Поглощение В классической электродинамике поглощение излучения средой описывается законом Бугера для энергетического потока монохроматического излучения. Полный энергетический поток B – энергия электромагнитного излучения, переносимая в единицу времени на всех длинах волн, есть интеграл от функции распределения потока F(n) по частотам (длинам волн) излучения
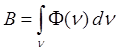 .
(3)
.
(3)
А F(n) выражается через объемную плотность энергии излучения r(n) соотношением
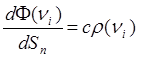 .
(4)
.
(4)
Закон Бугера для
монохроматического излучения, т. е. излучения в интервале частот ![]() , имеет вид:
, имеет вид:
![]() . (5)
. (5)
Здесь dЕa – поглощенная средой энергия излучения, равная
убыли энергетического потока, dl и dSn – элементарная длина поглощающей среды и
ее площадь, перпендикулярная направлению распространения излучения, 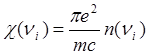 - коэффициент поглощения средой
монохроматического излучения на частоте ni, n(n) - распределение осцилляторов по частотам
поглощения. Для характеристики поглощения в классической электродинамике также
используется величина fna £1, которая
называется силой осциллятора в поглощении и находится из соотношения
- коэффициент поглощения средой
монохроматического излучения на частоте ni, n(n) - распределение осцилляторов по частотам
поглощения. Для характеристики поглощения в классической электродинамике также
используется величина fna £1, которая
называется силой осциллятора в поглощении и находится из соотношения ![]() . N – полное
число осцилляторов в единице объема среды. С учетом этого выражение для
поглощенной в единице объема среды энергии монохроматического излучения можно
записать в виде:
. N – полное
число осцилляторов в единице объема среды. С учетом этого выражение для
поглощенной в единице объема среды энергии монохроматического излучения можно
записать в виде:
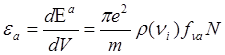 .
(6)
.
(6)
Таким образом, в классической электродинамике излучательная и поглощающая способности среды описывается силой осциллятора. Это безразмерная статистическая величина, представляющая собой долю осцилляторов, способных излучать или поглощать данную монохроматическую волну. При этом не учитывается природа самого осциллятора.
В квантовой механике испускание или поглощение монохроматических линий происходит в результате отдельных актов при переходе связанного электрона из одного стационарного состояния в другое. При этом излучается или поглощается фотон с энергией
![]() ,
(7)
,
(7)
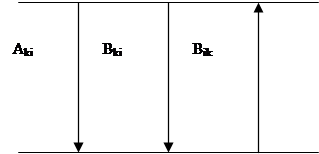
где h – постоянная Планка, Ei и Ek – энергии начального и конечного уровней оптического перехода соответственно (рис.1).
|
||||
 |
||||
|
||||
Рис.1. Схема энергетических уровней
А вопрос об излучении и поглощении решается путем введения вероятностей перехода – коэффициентов Эйнштейна: Bik – для поглощения, Bki – для вынужденного излучения и Aki – для спонтанного излучения. Т.е. в квантовой механике постулируется, что излучательные переходы могут быть спонтанными и вынужденными. Спонтанные переходы происходят самопроизвольно случайным образом, а вынужденные – под действием известной возбуждающей силы, например, под действием электромагнитного поля пролетающего мимо атома фотона с частотой nki. При этом число переходов в единицу времени в единице объема вещества определяется простыми соотношениями:
![]() ,
,
![]() ,
(8)
,
(8)
![]() .
.
Здесь r(nki) – плотность излучения на частоте перехода nki .Если эти соотношения помножить на энергию фотона hnki, то получатся выражения для мощности излучения и поглощения соответственно.
Входящие в эти
выражения коэффициенты Эйнштейна являются размерными величинами, а именно: ![]() . Величина tki = 1/Aki называется излучательным временем жизни k®i перехода, а величина
. Величина tki = 1/Aki называется излучательным временем жизни k®i перехода, а величина 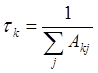 называется
излучательным временем жизни уровня k. Здесь
суммирование проводится по всем уровням j,
расположенным ниже уровня k.
называется
излучательным временем жизни уровня k. Здесь
суммирование проводится по всем уровням j,
расположенным ниже уровня k.
Все коэффициенты Эйнштейна, являясь константами оптического перехода и константами атома, связаны между собой. Эта связь просто находится в условиях термодинамического равновесия среды и излучения, когда заселенности уровней подчиняются закону Больцмана
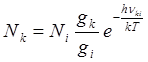 ,
(9)
,
(9)
а плотность излучения – закону Планка
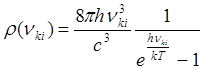 .
(10)
.
(10)
При высокой температуре T, когда exp(hnki/kT) >>1, находим
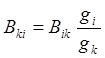 ,
(11)
,
(11)
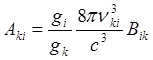 .
(12)
.
(12)
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.