Излучение и поглощение спектральных линий. Интенсивность и ширина спектральной линии, страница 3

1)  Малая оптическая плотность вещества излучателя, т.е. c(n_ki) l <<1. Разлагая экспоненту в ряд и ограничиваясь первым членом разложения, видим, что только в этом случае измеряемая интенсивность пропорциональна физической интенсивности.

Оптически плотная среда: c(n_ki) l >>1, тогда в числителе можно пренебречь экспонентой. В этом случае реализуется эффект насыщения поглощения и измеряемая интенсивность уменьшается c(n_ki) раз относительно физической интенсивности. При этом если излучающая среда находится в термодинамическом равновесии, то значения измеряемых интенсивностей всех монохроматических линий распределяются в соответствии с законом Планка. По этому распределению с высокой точностью можно измерять температуру вещества излучателя. При отсутствии термодинамического равновесия распределение измеряемых интенсивностей отдельных линий может быть любым.

Ширина спектральной линии. Спектральная линия является не бесконечно узкой, а имеет определенную ширину, которая математически описывается функцией S(n), называемой форм-фактором линии. Уширение линии происходит в результате внутренних причин, обусловленных природой атомов и молекул – естественная ширина линии, и внешних причин, обусловленных взаимодействием излучающего атома с внешней средой.

Естественная ширина линии вызвана конечной шириной энергетических уровней между которыми происходит оптический переход. Ширина уровня DE связана с его временем жизни t соотношением неопределенности Гейзенберга:

                                                                      (18)

Излучательное время жизни k-о уровня определяется, как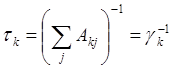. Учет ширины уровней приводит к тому, что контур линии (форм-фактор) описывается кривой Лоренца (рис.2)

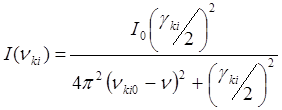,                                 (19)

где . Эта функция имеет максимум при n = n_ki0, а на расстояниях n -n_ki0 = ± γ_ki/4p спектральная плотность убывает в 2 раза. Величина Δn_n = γ_ki/2p называется естественной шириной линии. А в масштабе длин волн уширение равно: 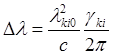. Ширина линий, излучаемых на переходе между короткоживущими уровнями (A_ki =10⁸ c^-1), составляет 10^-5 нм. Аномально широкими являются линии, верхний уровень которых близок к пределу ионизации. Их естественная ширина может достигать 0,1 нм.

Естественное уширение спектральных линий является основным фактором уширения только для свободных атомов и молекул, не взаимодействующих с другими частицами и полями. Если же частицы взаимодействуют друг с другом, т.е. находятся в состоянии газа, то время жизни их энергетических уровней уменьшается за счет столкновений. С точки зрения классической электродинамики столкновение приводит обрыву синусоиды излучаемой электромагнитной волны. «Оборванной» синусоиде соответствует уширенная линия. В этом случае контур линии описывается также кривой Лоренца при замене излучательного времени жизни  на t_c - среднее время между столкновениями. Исходя из кинетической теории газов, , где  - длина свободного пробега частицы,  - средняя скорость частицы, N₀ – концентрация частиц в газе, s~10^-16 см² - эффективное сечение столкновений, m – молекулярная масса частицы, R – газовая постоянная, T – абсолютная температура газа. Ширина контура определяется таким же образом, как и при естественном уширении. Она равна:

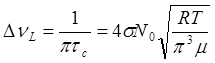.                                        (20)

Т.е. она зависит от давления в газе p через концентрацию частиц: p=N₀kT. Это уширение называется лоренцевским. При низком давлении газа, много меньшем атмосферного давления, лоренцевская ширина линии сопоставима с естественной, а при атмосферном давлении и выше она много больше естественной. Например, для l=500 нм и T =1000К при p=10^-3 атм. Dl_L » 1,8×10^-6 нм, а при p=1 атм. Dl_L » 1,8×10^-3 нм.

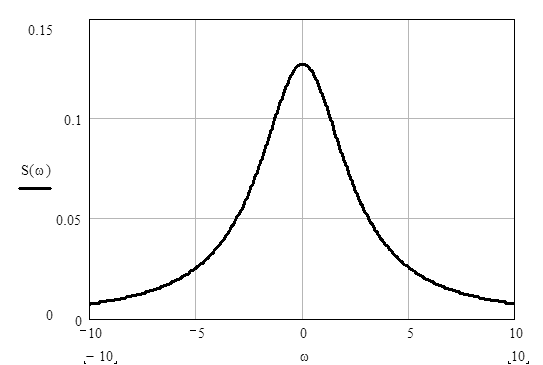
Рис.2. Характерный график кривой Лоренца S(ω) – контур спектральной линии

При хаотическом тепловом движении излучающих частиц форм-фактор определяется эффектом Доплера и описывается законом Гаусса, который наиболее просто записывается для циклической частоты w=2pn:

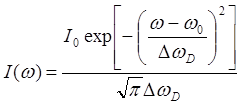,                                         (21)

где 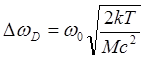, Т – абсолютная температура, М – масса частицы. Ширина контура на его полувысоте равна  , но часто доплеровской шириной называют непосредственно дисперсию Dw_D. Она зависит от температуры среды и по порядку величины сопоставима с лоренцевской шириной.