Т.к. столкнувшиеся частицы изменяют свою скорость, то они выбывают из пучка. Причем убыль частиц из пучка равна числу столкновений с обратным знаком. За счет этой убыли на расстоянии x поток частиц будет равен:
![]() .
(26)
.
(26)
Отсюда видно, что коэффициент Q0 имеет размерность площади. Он называется полным сечением столкновения атома с частицей. Так как столкновения могут носить упругий и неупругий характеры, вероятности которых соответственно равны Pe и Pjk, полное сечение столкновения можно представить в виде
![]() . (27)
. (27)
Величины ![]() и
и
![]() называются эффективными сечения
соответственно упругого и неупругого столкновения, переводящего атом с j уровня на k.
называются эффективными сечения
соответственно упругого и неупругого столкновения, переводящего атом с j уровня на k.
В зависимости от энергии налетающей частицы E эффективное сечение неупругого столкновения имеет экстремальный характер. Его максимум порядка 10-16 см2 достигается при Emax = (2-4) |Ek –Ej|, а при очень больших энергиях эффективное сечение спадает по закону Борна
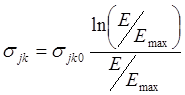 .
(28)
.
(28)
Так как в типичной плазме газового разряда кинетические энергии тяжелых частиц (атомов, ионов, молекул), как правило, значительно ниже Emax, а кинетические энергии свободных электронов порядка Emax, то в процессах возбуждения и девозбуждения уровней электроны играют гораздо большую роль, чем тяжелые частицы.
Литература.
М.А. Ельяшевич. Атомная и молекулярная спектроскопия. М.: Гос.изд-во физ.-мат. лит-ры, 1962, 892 с.
И.И. Собельман. Введение в теорию атомных спектров. М.: Гос.изд-во физ.-мат. лит-ры, 1963, 640 с.
С.Я. Фриш. Оптические спектры атомов. М.: Гос.изд-во физ.-мат. лит-ры, 1962, 792 с.
Лекция 3.
ИЗЛУЧЕНИЕ И ПОГЛОЩЕНИЕ СПЕКТРАЛЬНЫХ ЛИНИЙ. ИНТЕНСИВНОСТЬ И ШИРИНА СПЕКТРАЛЬНОЙ ЛИНИИ.
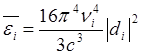 (1)
(1)
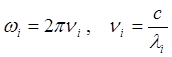 , di
= eai
, di
= eai
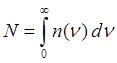 число осцилляторов, n(n) – их
распределение по частотам излучения. В интервале частот
число осцилляторов, n(n) – их
распределение по частотам излучения. В интервале частот ![]() ,излучают
,излучают
![]() осцилляторов, fni £1
осцилляторов, fni £1
![]() , (2)
, (2)
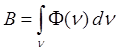 .
(3)
.
(3)
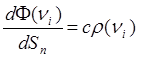 .
(4)
.
(4)
![]() . (5)
. (5)
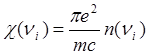
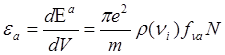 .
(6)
.
(6)
![]() ,
(7)
,
(7)
|
||||
 |
||||
|
||||
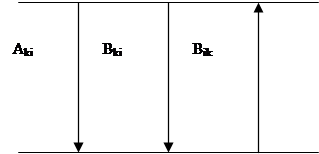
Рис.1. Схема энергетических уровней
![]() ,
,
![]() ,
(8)
,
(8)
![]() .
.
![]() . tki = 1/Aki
– излучательное время жизни k®i перехода,
. tki = 1/Aki
– излучательное время жизни k®i перехода, 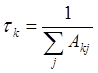 - излучательное время жизни уровня k.
- излучательное время жизни уровня k.
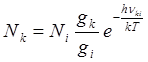 - закон
Больцмана (9)
- закон
Больцмана (9)
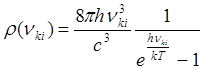 - закон
Планка (10)
- закон
Планка (10)
При exp(hnki/kT) >>1
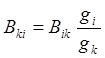 ,
(11)
,
(11)
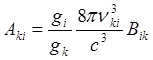 .
(12)
.
(12)
g=2J+1 – статистический вес (статвес) уровня
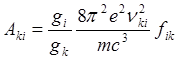 ,
(13)
,
(13)
![]() - правило сумм Томаса-Куна, N – числу валентных электронов
- правило сумм Томаса-Куна, N – числу валентных электронов
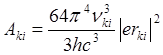 ,
(14)
,
(14)
D=e rki – дипольный момент перехода
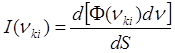 .
(15)
.
(15)
![]() - физическая
интенсивность (16)
- физическая
интенсивность (16)
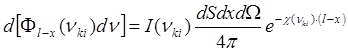 .
(17)
.
(17)
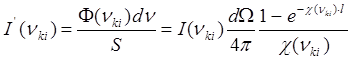 - измеряемая
интенсивность (18)
- измеряемая
интенсивность (18)
![]()
![]() (18)
(18)
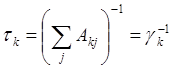 .
.
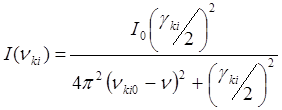 - кривая
Лоренца (19)
- кривая
Лоренца (19)
![]() . Δnn
= γki/2p или
. Δnn
= γki/2p или 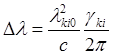 .-
естественная ширина линии.
.-
естественная ширина линии.
![]() ,
, ![]() ,
, ![]()
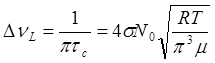 -лоренцевская
ширина (20)
-лоренцевская
ширина (20)
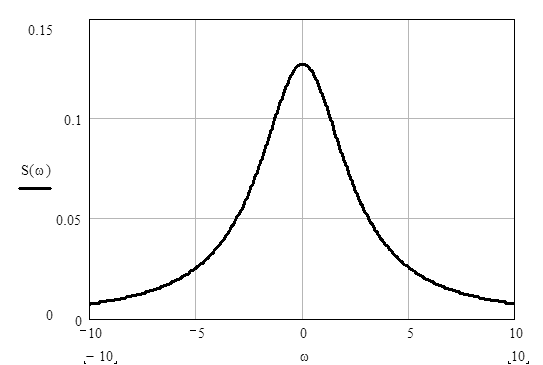
Рис.2. Характерный график кривой Лоренца S(ω) – контур спектральной линии
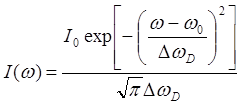 -
доплеровский контур (21)
-
доплеровский контур (21)
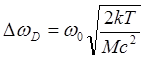 - доплеровская ширина.
- доплеровская ширина. ![]() - ширина контура на полувысоте.
- ширина контура на полувысоте.
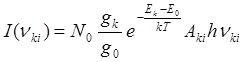 .
(22)
.
(22)
![]() ,
(23)
,
(23)
![]() .
(24)
.
(24)
![]() .
(25)
.
(25)
![]() .
(26)
.
(26)
![]() .
(27)
.
(27)
![]() и
и ![]() –
эффективные сечения упругого и неупругого столкновения.
–
эффективные сечения упругого и неупругого столкновения.
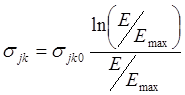 - закон Борна
- (28)
- закон Борна
- (28)
Emax = (2-4) |Ek –Ej|,
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.